Chapter 2
Models of Growth: Rates of Change
2.5 Modeling Population Growth
2.5.3 Slope Fields
We will learn here how to draw a picture of a differential equation that will help us understand what it means for a function to be a solution.
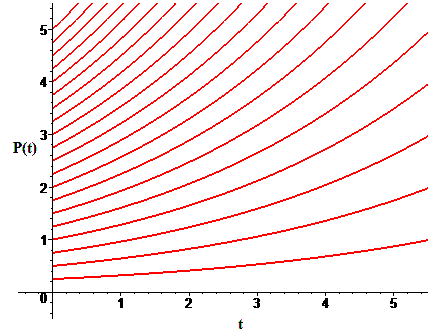
Figure 1 shows a number of solutions of the differential equation
\( \frac{dP}{dt}=0.25 P\).
If you tap the graph in Figure 1, you will see the same solutions, but only short segments of each solution curve. These short segments still give us a good idea of what the solution curves look like, and we could draw in the rest of the curves if we wanted to.
Notice that the curve segments in Figure 1 are nearly straight; i.e., they are essentially line segments. Here is the important point: We know what the slopes of these line segments must be from the differential equation. We do not need to know formulas for the solutions in order to determine slopes.
For this particular differential equation, we know that the slope of a very short piece of solution curve (a line segment) at any point \( (t,P)\) is \(0.25 P\). Thus, for example, the slope at \(( 1,2)\) is \(0.25 \times 2\) or \(0.5\), the slope at \((2,6)\) is \(1.5\), and so on.
This gives us a way to represent the differential equation
graphically without reference to its solutions: At lots of points in the plane we draw short line segments with slopes that match the equation. Figure 2 is such a picture: At each point \((t,P)\) on a closely spaced grid, we have drawn a small line segment whose slope is \(0.25 P\). The resulting picture is called a slope field.
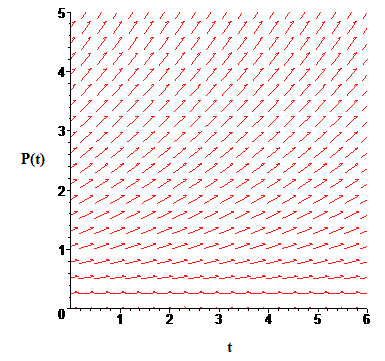
Figure 2 Slope field for dP/dt = 0.25 P
The selected points are only representative of the infinity of points in the \((t,P)\) plane, but they show us a clear picture of the slope field described by the differential equation. Any solution of the differential equation is a function \(P = P(t)\) whose graph passes through the slope field in the directions of the line segments it meets along the way. In Figure 3 we show the same field with several solutions superimposed.
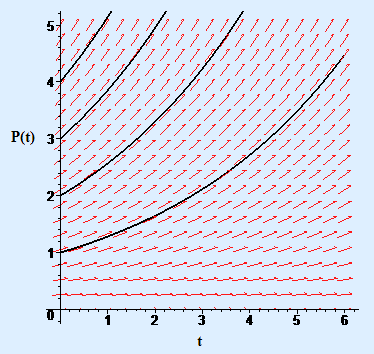
Figure 3 Slope field for dP/dt = 0.25 P with several solutions superimposed