2.6.4 Finding a Power Model

In the following example we show how to find a model function for data that appear to fit a power model.

Example

The Jurassic Toy Company produces seven models of their stuffed brachiosaurus. Each of the newer six models scales up the original successful model. Table 4 gives, for each model, the volume \(v\) of compressed stuffing required (in cubic inches) together with the scale factor \(x\). Find a model formula for \(v\) as a function of \(x\).

Solution   To check whether a power model is reasonable, we look at a log-log plot of the data and decide whether the plotted points lie close to a straight line. Figure 4 shows the plot for these data.

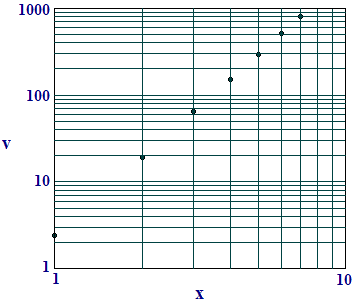
Now how do we find an appropriate model of the form

If we have such a model, then

Thus the straight line in the log-log plot should have slope \(r\). If we use the first and last points to determine the slope, then our choice of \(r\) should be

It looks like \(3\) is a reasonable power.

Now our model has the form $v=c{x}^3$. If we use, say, the fourth point to determine \(c\), we have

or

Our model function is

We show a plot of the data with the graph of this model function in Figure 5.

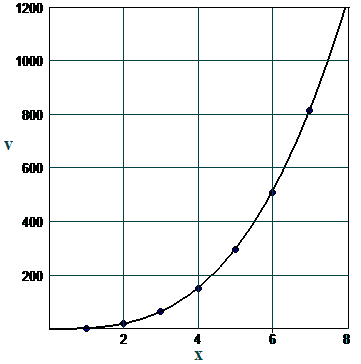
Image credit