In previous chapters we have investigated natural growth models incorporating differential equations of the form

In these models, if \(k\) is positive, growth increases without bound. If \(k\) is negative, we have decay to a zero steady-state. In both cases, we need exponential functions to describe the solutions explicitly.

In this section we consider models of oscillating or vibrating phenomena. A classic example of this is periodic motion, exemplified by the repeating motion of a mass bobbing up and down on the end of a spring. That may not sound like an important problem — unless you have an old car in which the shock absorbers are really shot — but it serves nicely as a prototypical oscillation, one that we can easily observe and measure. It's much harder to observe the crystals in our watches, the electrical current in our walls, or the silicon circuits in our computers. And study of the bouncing mass on a spring is the beginning of analyses of phenomena such as vibrations of a bridge or the flutter of a sail or an airplane wing.

Just as natural growth leads to exponential functions to describe them, so vibrations and oscillations lead to sine and cosine functions. We will consider those functions next in this section.

5.3.1 Spring Mass Systems

We begin our study of the spring-mass system with a physical law — a property of springs that has been observed and measured in many physics labs.

Hooke's Law   The force required to stretch a spring a distance \(s\) from its natural length is proportional to \(s\).

The law asserts that the force function has the form \(F(s)=ks\) for some constant \(k\), called the spring constant for the given spring. To find the spring constant, we can hang a known weight on the spring and measure the amount of displacement. For example, if a \(5\)-pound weight stretches a spring \(6\) inches, then (in English units of feet and pounds), \(5=k\,\times\,0.5\), so the spring constant \(k\) is \(10\) lbs/ft.

Click on the image at the right to see a demonstration of Hooke's Law by Brian Andersson, School of Physics and Astronomy, University of Minnesota. Used by permission.

Weight means the force exerted on an object by gravity. By Newton's Second Law, this force is the mass of the object times the acceleration \(g\) due to gravity. Thus, weight \(w\) and mass \(m\) are related by

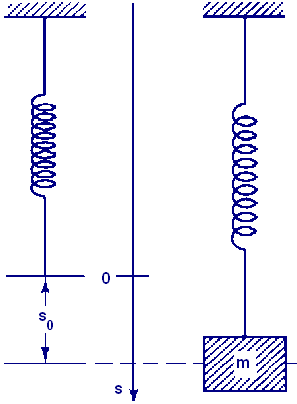
In Figure 1 we show two views of the same spring, one at its natural length (no force being applied) and the other stretched by hanging an object of mass \(m\) on it. We assume the spring-mass system is in equilibrium in the second view, i.e., the object is not moving. Thus, the force the spring exerts on the object exactly balances the gravitational force the object exerts on the spring, namely, \(mg\). By Hooke's Law, this force is also \(ks_0\), so the mass, spring constant, and equilibrium displacement are related by

Now we consider what happens if we stretch the spring an additional distance \(x\), as in Figure 2. (Think of rescaling the vertical axis additively so that the new origin \(x=0\) is at \(s=s_0)\). The system consisting of just the mass and spring is no longer in equilibrium. If we let go, there will be an imbalance of forces that will cause the object to move. On the one hand, there is the gravitational force \(mg\) — positive because our positive direction is downward. On the other hand, there is the restoring force of the spring, which, according to Hooke's Law, is \(-ks=-k(x+s_0)\), negative because this force opposes increase in \(s\). Thus, the total force on the object is \(mg-kx-ks_0\), which simplifies (because \(mg=ks_0\)) to just \(-kx\).

Click on the image at the right to see a demonstration of spring-mass motion by Brian Andersson, School of Physics and Astronomy, University of Minnesota. Used by permission.