Chapter 5
Modeling with Differential Equations





5.3 Periodic Motion

5.3.3 Circular Motion: Sines and Cosines

Imagine a circular running track of radius one hundred meters, and imagine an \(xy\)-coordinate system placed on the track with the center of the circle at the origin. (See Figure 3.) Suppose you start at the point with coordinates \(x=100\) and \(y=0\) and run in a counterclockwise direction with a speed of five meters per second. How can we describe your position as a function of the angle \(\theta\) between your line to the origin and the \(x\)-axis? How can we describe your position as a function of time?

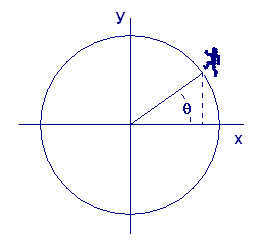Figure 3   Position of a runner on a track of \(100\) meters

Consider first the question of describing your position in terms of \(\theta\). We'll measure the angle in radians, so one lap corresponds to \(2\pi\) radians, a quarter lap to \(\pi/2\) radians, and so on. To locate your position in the plane, we need to specify both the \(x\)- and \(y\)-coordinates. The functions that do this should be old friends — or at least passing acquaintances. If you have traveled through an angle of \(\theta\) radians, then you are located at the point with \(x\)-coordinate \(100\cos(\theta)\) meters and \(y\)-coordinate \(100\sin(\theta)\) meters. That is,

x = 100 ⁢   cos ( θ ) ,

and

y = 100   sin ( θ ) ⁢ .

Checkpoint 1 Checkpoint 1

In Figure 4, we show another circle of radius \(100\) with separate graphs of the \(x\)- and \(y\)-coordinates (as functions of the central angle \(\theta\)) that result from motion around the circle.

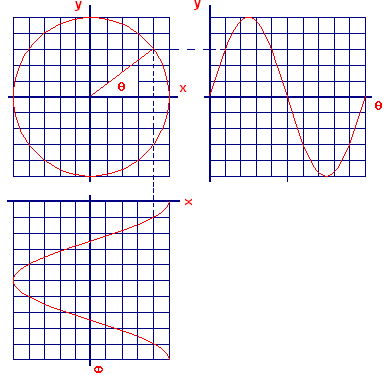Figure 4   Generation of sine and cosine functions from motion around a circle

Notice that the axes for the \(x\)-coordinate graph are rotated \(\pi/2\) radians (90°) clockwise from the usual position. In Figure 5 we show the left half of Figure 4 rotated counterclockwise \(\pi/2\) radians.

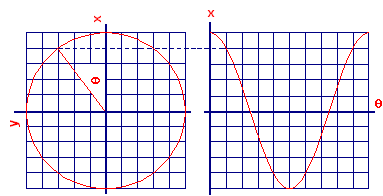Figure 5   Generation of cosine function from motion around a circle

Activity 2

  1. With Figure 4 on the screen, put the index finger of your left hand on the circle at the point \((100,0)\) and the index finger of your right hand on the graph of the \(y\)-coordinate at the point \((0,0)\). As you move your left finger along the circle, let your right finger trace out the graph of \(y\) as a function of \(\theta\).
  2. With Figure 5 on the screen, place your left index finger at the point \((0,100)\) on the \(x\)-coordinate graph and your right index finger on the circle at the point \((100,0)\). As you move your left finger along the circle, let your right finger trace out the graph of \(x\) as a function of \(\theta\).

You have just experienced the generation of the sine and cosine functions from motion around a circle.

Checkpoint 2 Checkpoint 2

Now we turn to the question of your location on the track as a function of time in seconds. Let \(t=0\) correspond to your starting position at \(x=100\) and \(y=0\). Answer the questions in Checkpoint 3 and find the formulas requested.

Checkpoint 3 Checkpoint 3

Activity 3

  1. What circle is traveled by a moving object with coordinate functions \(x=\cos(\theta)\) and \(y=\sin(\theta)\)? (This circle is called the unit circle.)

Explain the following facts about sine and cosine:

  1. For every angle \(\theta\), \(\cos(\theta + 2 \pi)=\cos(\theta)\).

  2. For every angle \(\theta\), \(\sin(\theta + 2 \pi)=\sin(\theta)\).

  3. For every angle \(\theta\), \(\sin^2(\theta)+\cos^2(\theta) =1\).

  4. For every angle \(\theta\), | sin ( θ ) | ≤ 1.

  5. For every angle \(\theta\), | cos ( θ ) | ≤ 1.

Comment 3Comment on Activity 3

Checkpoint 4Checkpoint 4

Image credit
Go to Back One Page Go Forward One Page

Go to Contents for Chapter 5Contents for Chapter 5