5.5.3 Inverse Trigonometric Functions

We repeat here the graphs of two of our trigonometric functions, sine and tangent.

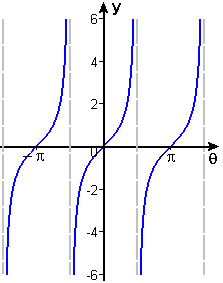Figure 8   \(y = \sin\theta\)	Figure 9   \(y = \tan\theta\)

It is immediately evident from the graphs that neither of these functions has an inverse function, because neither can pass the "horizontal line test" — that is, for a given \(y\) value (in the range of the function), there is more than one \(\theta\) value. Indeed, every periodic function of \(\theta\) has infinitely many \(\theta\) values for each \(y\) value — and therefore cannot have an inverse function. Now, this may fly in the face of your past experience, because you are surely familiar with the phrase "inverse trig function" — your calculator even has buttons for such functions.

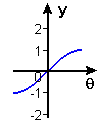
As we saw in Chapter 1 with the squaring function, the secret to defining inverse trig functions is to reduce their respective domains to ones in which each \(y\)-coordinate occurs exactly once. For the sine function, this is accomplished by using the domain \(-\frac{\pi}{2} \leq \theta \leq \frac{\pi}{2}\), and for tangent, we use the open interval \(-\frac{\pi}{2} < \theta < \frac{\pi}{2}\). These restricted-domain functions are shown in Figures 10 and 11.

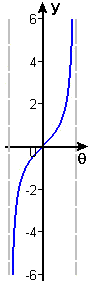Figure 10   \(y = \sin\theta\), \(-\pi/2 \leq \theta \leq \pi/2\)	Figure 11   \(y = \tan\theta\), \(-\pi/2 < \theta < \pi/2\)

Now we will see one of the ways an inverse of a trigonometric function can be useful.

Example 3   The designer for an art museum is laying out a room for display of a famous large painting that measures 5 feet high by 12 feet long, and that will be hung with its bottom edge 6 feet from the floor. The preferred viewing place in the room will be a bench to be placed at a distance \(A\) from the wall. If the average (seated) viewer's eyes are 4 feet above the floor, what should the distance \(A\) be in order to maximize the viewing angle \(\theta\) (see Figure 12)?

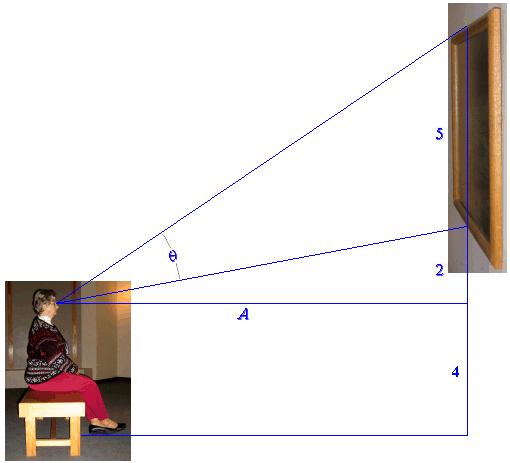
Figure 12   Picture at an exhibition

Solution (partial)   In Figure 13 we have extracted the essential features of Figure 12.

Figure 13   The viewing angle

The distance \(A\) is one side of a right triangle that is made up of two other triangles. From these two triangles, we see that

\(\tan(\theta + \phi)=\frac{7}{A}\)   and   \(\tan(\phi)=\frac{2}{A}\).

If we take inverse tangents of both sides of both equations, we find

\(\theta+\phi=\tan^{-1}\left(\frac{7}{A}\right)\) and \(\phi=\tan^{-1}\left(\frac{2}{A}\right)\).

When we subtract the second equation from the first, we get a formula for \(\theta\) as a function of \(A\):

\(\theta=\tan^{-1}\left(\frac{7}{A}\right)-\tan^{-1}\left(\frac{2}{A}\right)\).

We show a graph of this function in Figure 14.

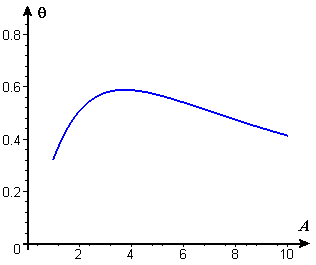
Figure 14   Viewing angle as a function of distance from wall

Not surprisingly, if the bench is either too close to the wall or too far away, the viewing angle is small, and there is a single maximum point at a distance of just under 4 feet. To locate the maximum exactly — which may or may not be important to the designer — we need a formula for the derivative of the inverse tangent (or "arctangent") function so we can find where the derivative takes the value \(0\).

In the process of finding the derivative of the arctangent, we use the derivative of the tangent — which we just saw (on the preceding page) is the square of the secant function.

Activity 6

There are two ways to find a formula for the derivative of the arctangent function:

1. Use implicit differentiation and the inverse relationship

   \(\tan\left(\tan^{-1}x\right)=x\).

2. Use the formula for differentiation of an inverse function.

Do it both ways, and confirm that both lead to the same formula.

Comment on Activity 6

Solution for Example 3 (continued)   Now that we have a formula for the derivative of the arctangent function, we can complete the calculation of a maximum value for \(theta\) as a function of \(A\):

d ⁢ θ d ⁢ A	= d d A [ tan -1 ( 7 A ) - tan -1 ( 2 A ) ]
	= 1 1 + ( 7 A ) 2 ⁢ d d A 7 A - 1 1 + ( 2 A ) 2 ⁢ d d A 2 A
	= 1 1 + ( 7 A ) 2 ⁢ ( - 7 A 2 ) - 1 1 + ( 2 A ) 2 ⁢ ( - 2 A 2 )
	= - 7 A 2 + 49 + 2 A 2 + 4

This last expression is \(0\) when \(2 A^2+98=7 A^2+28\), that is, when \(A^2=14\). The positive solution for \(A\) is \(\sqrt{14}\), or about \(3.74\) (feet), which is in agreement with Figure 14.

Checkpoint 3

Activity 7

Follow the pattern of Activity 6 to find a derivative formula for the arcsine function. You will need to use the relationship between the arcsine and the arccosine, which is illustrated in Figure 15. In the Figure, \(y=\sin^{-1}x\) — read this as "\(y\) is the angle whose sine is \(x\)." Then you need to fill in the blank in "\(y\) is the angle whose cosine is ________." You will see where you need this in the derivative calculation.

Figure 15   \(y=\sin^{-1}x\)

Comment on Activity 7