8.6.3 Integrating Fractional Powers

Some very simple physical and mathematical situations can lead to integrals that involve fractional powers such as the square root (\(1/2\) power). For example, in Project 1 at the end of this chapter, we explore the problem of finding distance along a curved path, namely, the graph of \(y=x^2\), and we see that distance between any two points is a definite integral of y = 1 + 4 ⁢ x 2 . If we want to apply the Fundamental Theorem of Calculus to this problem, we need to know an antiderivative of this function.

Example 2

Both Wolfram|Alpha and Sage compute

∫ 1 + 4 ⁢ x 2 d x = 1 2 ⁢ x ⁢ ⁢ 1 + 4 ⁢ x 2 + 1 4 sinh - 1 ( 2 x ) + C .

This integral doesn't look very difficult to evaluate, and yet the answer looks rather complicated. The inverse hyperbolic sine function, \(\sinh^{-1}\) or arcsinh, is defined and its derivative calculated in Project 1 in Chapter 5. Earlier in this chapter, in Problems 2 and 3 in Section 8.4, we explored a "tangent substitution" that would appear to be the first step in evaluating this integral. But it is not at all clear how that transformation might lead to an inverse hyperbolic function in the answer. To get a sense of what's involved in solving this problem, go back to the Wolfram|Alpha page and click on "Step-by-step solution". This may give you some sense of the power of our CAS tools.

Example 3

Figure 1  An indefinite integral

Here is a subtly different indefinite integral:

∫ 1 + 4 ⁢ x 3 d x

You can easily modify both the Sage interact and the Wolfram|Alpha command in Example 2 to find out what they will report as an answer. However, Sage doesn't change the integral at all, and Wolfram|Alpha reports an answer that involves something called an "elliptic integral" (a topic beyond the level of this course), as well as imaginary numbers (square roots of \(-1\)). The fact is, this integral cannot be expressed in terms of "elementary" functions, i.e., the functions we study in this course. Non-elementary functions are no help here.

Keep in mind that there is a simpler way to express the indefinite integral by a formula that comes from the Fundamental Theorem of Calculus:

∫ 1 + 4 ⁢ x 3 d x = ∫ 0 x 1 + 4 ⁢ t 3 d t + C

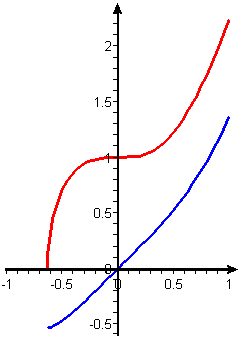
For any choice of \(C\) (e.g., \(C=0\)), the right-hand side defines a function \(F(x)\) that can be evaluated (numerically) at any \(x\) in the domain. The points \((x,F(x))\) can be graphed, as in Figure 1, which shows the graphs of \(f(x)=\sqrt{1+4x^3}\) (in red) and \(F(x)\) (in blue).

Checkpoint 1

Activity 2

As we noted at the start of this page, Project 1 develops a formula for length of the graph of a function, \(f(x)\), from \(x=a\) to \(x=b\):

Length of curve ⁢ = ∫ a b 1 + [ f ′ ( x ) ] 2 d ⁢ x .

We will apply that formula in this activity to find the length of \(f(x)=\ln\,x\) from \(x=1\) to \(x=4\). See Figure 2, in which this segment of the graph is highlighted in blue.

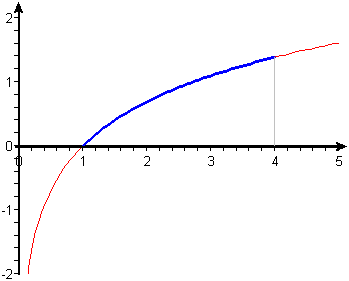
Figure 2  The graph of the natural logarithm function

1. Estimate the length of the curve by finding the length of the line segment from \((1,0)\) to \((4,\ln\,4)\). This estimate will be a check on your calculation by an integral.
   
   
2. Show that the length is given exactly by

∫ 1 4 1 + 1 x 2 d ⁢ x .

3. Change the function definition in the Sage interact from Example 2 to calculate the indefinite integral

∫ 1 + 1 x 2 d ⁢ x .

4. Explain why the integral in part c can be rewritten as

   ∫ x 2 + 1 x d ⁢ x .

   Modify your function definition to compute this form of the integral. Observe that the answer is now expressed more simply, but the check is not very convincing. (No matter — we already checked it in part c.)
   
   
5. Use one of your answers from parts c and d to complete the calculation of the definite integral in part b. Compare your result to your estimate in part a. If your calculation of the curve length is not reasonable, find your error and correct it.

Comment on Activity 2

Activity 2 illustrates the continued need for pencil-and-paper (or mental) algebra skills, even when you are using a computer algebra system — especially when you are using a computer algebra system. No existing CAS incorporates all human intelligence and experience in manipulating mathematical symbols.

Activity 2 is also an "artificial" use of CAS, in the sense that you could ask our Sage Definite Integral tool or Wolfram|Alpha (or a hand-held calculator) directly for the value of the definite integral in part b. It matters very little whether the numerical answer comes from a numerical integration (e.g., Simpson's Rule) or an application of the Fundamental Theorem. It matters a lot how hard you have to work to get that answer, and that is another aspect of choosing the right tool for the job.