8.6.6 Different Answers to the Same Problem

The Fundamental Theorem of Calculus tells us that a given continuous function has infinitely many antiderivatives, but any one differs from any other only by an additive constant. On the other hand, integration of the same function by different computer algebra systems can produce answers that look very different. And even with a single CAS, integration of a function expressed in different ways can produce answers that look different. (See Activity 1 for an example.) This is not really a problem, as long as we can differentiate the answers to confirm that they really are antiderivatives. But the results can be unsettling, especially since there are significant opportunites to make mistakes entering functions in the CAS, and a different-looking answer may really be a different answer (by more than an additive constant). Here we consider some examples and explore another way to tell if different-looking answers are both correct.

Example 5

In Figure 3 we show (with the help of Wolfram|Alpha) the graphs of four functions.

Note the apparent parallel property of all four graphs, which strongly suggests that any two of these functions differ only by an additive constant. Thus the four functions should all be antiderivatives of the same function. Or, to put it another way, the four functions should all have the same derivative. But the formulas don't look as though the functions all have the same derivative. We explore that issue in the next Activity.

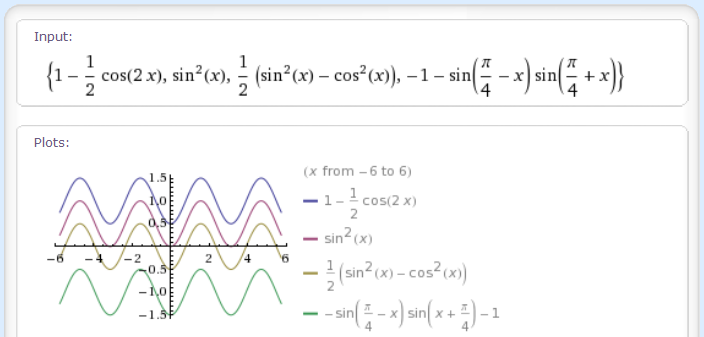
Figure 3. Functions that differ from each other by additive constants.

Activity 6

1. Here are the four functions in Figure 3:

   \(f_1(x)=1- \frac{1}{2} \cos(2x)\)

   \(f_2(x)=\sin^{2}(x)\)

   \(f_3(x)=\frac{1}{2} [\sin^{2}(x)-\cos^{2}(x)]\)

   \(f_4(x)=-1- \sin (\frac{\pi}{4}-x) \sin (\frac{\pi}{4}+x)\)

   Calculate the derivative of each of these functions. (You may use the Derivative tool if you wish.) How many of these functions appear to have the same derivative?
2. Use the Graph tool to plot the four derivative functions on the same set of axes. Now how many of the four derivatives appear to be the same?
   
3. Use the Graph Difference tool to plot \(f(x)-g(x)\) for each pair \(f(x)\) and \(g(x)\) of the four original functions. Does this confirm that the two functions differ by a constant?

Comment on Activity 6

Checkpoint 4

We see from the Example, Activity, and Checkpoint that there are a number of ways a CAS could produce different (or different-looking) answers for the same integral. More important, we see that we can easily check that different-appearing answers are both correct, in at least two ways:

1. Differentiate each answer to confirm that it is an antiderivative. (This should be a routine checking step in any case.)
2. Confirm that different-appearing algebraic forms differ by a constant by asking the CAS to graph their difference.

If the differentiations in step 1 produce different-looking algebraic forms, and there isn't any obvious way to confirm they are equivalent, then use the strategy of step 2 — ask the CAS to graph their difference, and confirm that it is \(0\).