Chapter 2
Models of Growth: Rates of Change
 2.1
Rates of Change
2.1
Rates of Change
Exercises
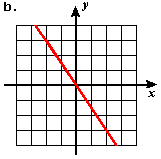
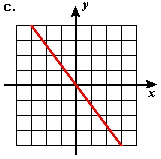
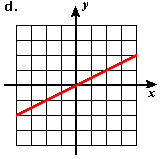
- Estimate the slope of each of the following lines.
In Exercises 2-11, find an equation of the given line in the \(x\),\(y\)-plane:
- The line with slope \(1.5\) through the point \((-1, 2.3)\).
-
The line through the points \((2.1, 1.7)\) and \((-1.5, 4.2)\).
-
The line with slope \(1 / 2\) through the point \((5,-2)\).
-
The line through the points \((3, -7)\) and \((1,-3)\).
-
The line with slope \(-1.7\) through the point \((1.5,-3.2)\).
-
The line through the points \((1.3,-0.7)\) and \((1.5,-3.2)\).
- The line through the point \((12,14)\) that is parallel to the \(x\)-axis.
- The line through the point \((5,4)\) that is parallel to the line \(4x+5y=3\).
- The line through the point \((5,4)\) that is parallel to the line through the points \((-1,6)\) and \((5,5)\).
- The line through the point \((-9,11)\) that is parallel to the line \(2x-5y+7=0\).
-

Our pop-up calculator (click on image at right) operates in radian mode. Find the average rate of change of the sine function (use the

button) over each of the following intervals.
| a. \([0,\pi / 4]\) |
b. \([0,\pi / 2]\) |
c. \([0,\pi]\) |
d. \([\pi / 2,\pi]\) |
- Find the average rate of change of the cosine function (see Exercise 12 — use the
 button) over each of the following intervals.
button) over each of the following intervals.
| a. \([0,\pi / 4]\) |
b. \([0,\pi / 2]\) |
c. \([0,\pi]\) |
d. \([\pi / 2,\pi]\) |


 Contents for Chapter 2
Contents for Chapter 2
 2.1
Rates of Change
2.1
Rates of Change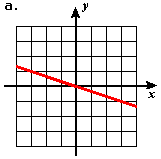
 button) over each of the following intervals.
button) over each of the following intervals. button) over each of the following intervals.
button) over each of the following intervals.
