2.4.3 The Natural Base

We summarize what we know so far about derivatives of exponential functions. For a given \(b\), we have

d d t b t = L ( b ) b t ,

where \(L(b)\) is the value of the derivative at \(t = 0 \). This number also may be described as

This description of \(L(b)\) defines it as a function of \(b\) but does not tell us how to find values of that function. In the Activities and Checkpoints on the preceding page, you determined six such values approximately, those for \(b = 2, 3, 4, 5, 6, \) and \(7 \). We plot this scanty information about \(L(b)\) as a function of \(b\) in Figure 1.

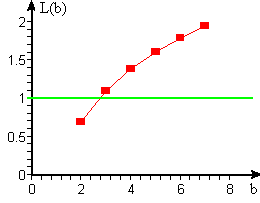
Figure 1   Selected values of L(b)

Activity 4   Figure 1 suggests the possibility of a smooth curve that passes through the points ( b , L ( b ) ) for \(b=2, 3, 4, 5, 6, \) and \(7\). To enhance this suggestion, we have “connected the dots” with straight-line segments that should approximate such a curve. The figure also suggests a way to finish our derivative calculation, at least for one base \(b\), without having to calculate \(L(b)\). Specifically, the curve suggested in Figure 1 crosses the horizontal line \(L(b) = 1\) for some \(b\). Estimate from your graph about how big \(b\) has to be to make \(L(b) = 1\).

Comment on Activity 4

Now we will carry out an experiment by which you can determine more precisely that value of \(b\) for which \(L(b) = 1\). In the Sage activity below, we provide a window on the graph of \(f(t) = b^t\) (shown in red) and an approximation \(g(t)\) to its derivative (shown in blue). The initial picture has \(b=2\), and the functions are graphed on the interval \([3,5]\). Click the Zoom Graph button, and take a moment to familiarize yourself with the following features of the activity.

• Just below the input box for \(b\) and the zoom slider are the function definition for \(f(t)\), the values of \(f(4)\) and \(g(4)\) [the difference quotient approximating \(f'(4)\)], and the ratio of these values, \(g(4)/f(4)\). The step size for the difference quotient defining \(g(t)\) is \(\Delta t = 10^{-8}\), a very small number.
• The choice to evaluate our functions at \(t = 4\) is entirely arbitrary. We know already that the ratio of \(f'(t)\) to \(f(t)\) is constant, namely, \(L(b)\), so the ratio will be the same no matter where we evaluate the functions. The starting value for the ratio, with \(b=2\), is \(L(2)= g(4)/f(4) = 0.693\).
• Our zoom function in this activity shrinks the interval size by a factor of \(1/10\) instead of the the factor of \(1/2\) that we have used in previous zooms. Because you will be zooming in much faster, the zoom slider has only six steps

Activity 5   Vary the value of \(b\) to get \(L(b) \) as close as you can to \(1 \). When your value of \(b\) is too small, the graph of \(b^t\) will be below the graph of its derivative. When it is too large, the graph of \(b^t\) will be on top. When you think you have the two curves coinciding, zoom in — you are likely to find that your \(b\) is still too small or too large. [Note: You can't expect to find more than 6 or 7 digits of the desired base, because after several zooms, Δ ⁢ t is no longer “small” relative to the interval on which you are calculating.]

The special number \(b\) for which you have found the first few decimal places is called the natural base for exponentials. The entire world of science and technology knows this number as \(e\). This symbol for the natural base was first used by the eighteenth-century Swiss genius Léonhard Euler (pronounced “oiler”).

The exponential function with \(e\) as its base has a special name.

Now we can see what is natural about the natural exponential function: Recall the formula for differentiating exponential functions:

d d t b t = L ( b ) b t .

If we replace \(b\) by \(e\) and \(L(b)\) by \(1\) we have

d d t e t = e t .

Thus the derivative of exp is itself, not just proportional to itself. In particular, we don't need to find the limiting value of ( b Δ ⁢ t - 1 ) / Δ ⁢ t to complete this derivative calculation.

Contents for Chapter 2