Exercises

1. Solve the differential-equation-with-initial-value problem

\(\displaystyle \frac{dP}{dt}=0.25 P\)  with \(P=2000\) at \(t=1\).

Solve each of the following differential-equation-with-initial-value problems (Exercises 2-9).

2. \(dP/dt=0.12 P\)   with \(P=500\) at \(t=0\)
3. \(dP/dt =-0.12 P\)   with \(P=500\) at \(t=0\)
4. \(dP/dt =0.12 P\)   with \(P=500\) at \(t=2\)
5. \(dP/dt =-0.12 P\)   with \(P=500\) at \(t=2\)
6. \(dy/dt=0.35 y\)   with \(y=100\) at \(t=0\)
7. \(dy/dt =-0.35 y\)   with \(y=100\) at \(t=0\)
8. \(dy/dt = 0.35 y\)   with \(y=100\) at \(t=1\)
9. \(dy/dt = -0.35 y\)   with \(y=100\) at \(t=1\)
10. Solve each of the following equations for \(t\).

a.  \(100=27 e^{0.07 t}\)

b.  \(200=33 e^{0.14 t}\)

c.  \(P=P_0 e^{k t}\)

d.  \(y=A e^{-\alpha t}\)

11. The function \(y=y_0 e^{k t}\) models continuous growth at a rate proportional to the amount present, with proportionality constant \(k\).
    
    
    1. Find the constant \(k\) that produces 2% growth in one time period. (Hint: Set \(t=1\) and \(y=1.02 y_0\). Solve for \(k\).)
       
       
    2. Find the constant \(k\) that produces \(r\)% growth in one time period.
12. A town with a population of 10,240 at the start of a year has an average growth rate of 5% per year.
    
    

    1. What is the population at the end of that year?
       
    2. What is the population halfway through the next year?
       
    3. What is the population halfway through the third year?
       
13. 
    1. A biologist has a colony of bacteria that contains 1.5 biomass units when first weighed and 1.95 biomass units an hour later. What is the biomass of the colony \(t\) hours later?
       
    2. Her first measurement was made at 8:30 A.M. and her last just before she went home at 4:30 P.M. Estimate the last measurement.
    
    
    
    
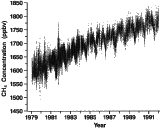14. “In recent years there has been a rise in the concentration of atmospheric methane of more than 1 percent per year. The increase is both rapid and significant because . . . methane is 20 times as effective as carbon dioxide in trapping heat.” Assuming that pattern continues without change, how long will it take to increase the concentration of atmospheric methane by 50%? (The answer is not “50 years.”)
    
    Source of quote: “Global Climatic Change” by R. A. Houghton and G. M. Woodwell, Scientific American, April 1989, pp. 36–44. Source of image: Oak Ridge National Laboratory
15. Suppose you deposit \(\$\)1000 in an account that pays 6.5% interest compounded annually, and you leave it (and the interest) there indefinitely.
    1. What is your balance one year after you made the deposit?
    2. By what factor has your money increased?
    3. What is your balance two years after the initial deposit?
    4. What is your balance 20 years after the initial deposit?
    5. What is your balance \(t\) years after the initial deposit?
16. Answer the same questions as in Exercise 15
    1. if the interest is compounded quarterly.
    2. if the interest is compounded monthly.
    3. if the interest is compounded daily.
17. This spring, after cubs were born, the bear population of Big Bear Natural Wilderness Area was 251, half of them female. Each spring 65% of the females each produce two cubs, and 50% of all the cubs are female. Assuming no deaths, estimate the bear population in 3 years. Give your answer in “whole” bears.