Chapter 2
Models of Growth: Rates of Change
2.5 Differential-Equation-with-Initial-Value Problems
In each of Problems 1-6, we show a slope field for a differential equation. For each problem, select one or more functions from the following list that could be a solution of that differential equation, and explain why.
| a. \(P(t)=1+t+3 e^t\) | b. \(P(t)=\frac{10}{10-t}\) | c. \(P(t)=3 e^{\,t/4}\) |
| d. \(P(t)=2+t^2/2-t^3/9\) | e. \(P(t)=2-t^2/4+t/2\) | f. \(P(t)=2-t^2/4+t^4/2\) |
| g. \(P(t)=\frac{10}{6-t}\) | h. \(P(t)=t^2/2-t^3/9+3\) | i. \(P(t)=2 e^t +t+1\) |
| j. \(P(t)=t^2/4-t+3\) | k. \(P(t)=3+e^{\,t/4}\) | l. \(P(t)=2-t+t^2/4\) |
1. 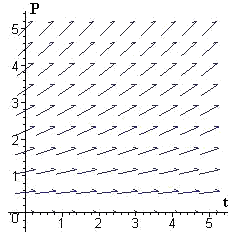 |
2. 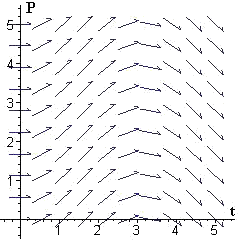 |
3. 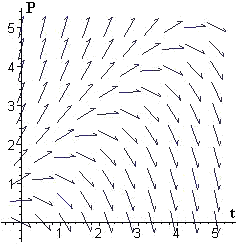 |
4. 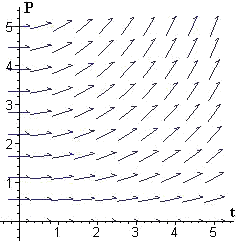 |
5. 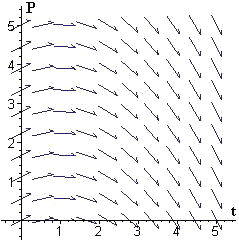 |
6. 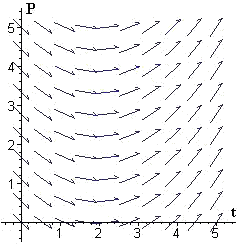 |
-
- Write down three functions that are solutions of the differential equation
- Describe the infinite family of functions that satisfy the differential equation in part (a).
- Solve the differential-equation-with-initial-value problem
- Solve the differential-equation-with-initial-value problem
\(dP/dt=0.02 P\).
\(dP/dt=0.02 P\) with \(P=5\) at \(t=0\).
\(dP/dt=0.02 P\) with \(P=5\) at \(t=2\).
-
- Write down three functions that are solutions of the differential equation
- Describe the infinite family of functions that satisfy the differential equation in part (a).
- Solve the differential-equation-with-initial-value problem
- Solve the differential-equation-with-initial-value problem
\(dP/dt=0.5 P\).
\(dP/dt=0.5 P\) with \(P=2\) at \(t=0\).
\(dP/dt=0.5 P\) with \(P=2\) at \(t=5\).
- Show that the general differential-equation-with-initial-value problem
-
 A town with a population of 10,240 at the start of a year has an average growth rate of 5% per year.
A town with a population of 10,240 at the start of a year has an average growth rate of 5% per year.
- What is the population at the end of that year?
- What is the population halfway through the next year?
- What is the population halfway through the third year?
- Explain your strategy for answering these questions.
- What is the population at the end of that year?
- A bank offering 6.5% compounded daily might advertise an “effective yield” of 6.7%. What does that mean?
- Some banks advertise continuous compounding of interest. This means (or should
mean) that the instantaneous rate of change of your balance is the advertised
interest rate times the balance. Suppose you deposit \(\$\)1000 in an account
that pays 6.5% interest compounded continuously, and you leave it (and the interest)
there indefinitely.
- What is your balance one year after you made the deposit?
- By what factor has your money increased?
- What is your balance two years after the initial deposit?
- What is your balance 20 years after the initial deposit?
- What is your balance \(t\) years after the initial deposit?
- How much difference is there between daily compounding and continuous compounding? In particular, what is the effective annual yield if the interest is compounded continuously?
- Relate your computations in Problems 11 and 12 to the statement
The limiting value of \((1+k \Delta t)^{1/\Delta t}\) as \(\Delta t \to 0\) is \(e^k\).
What specific values of \(k\) and \(\Delta t\) were you using?
-
 The First National Bank offers \(6\frac{1}{4}\)% interest on long-term deposits compounded daily, the Merchants and Farmers Bank offers \(6\frac{3}{8}\)% compounded quarterly, and the Central Bank offers \(6\frac{1}{2}\)% compounded annually.
The First National Bank offers \(6\frac{1}{4}\)% interest on long-term deposits compounded daily, the Merchants and Farmers Bank offers \(6\frac{3}{8}\)% compounded quarterly, and the Central Bank offers \(6\frac{1}{2}\)% compounded annually.
- Which bank would you choose if you planned to deposit a substantial amount of money in a long-term savings account?
- Can you think of a reason to split your deposit between two (or more) of the banks?
-
 An important concept in business and banking is the time required for an investment to double. A common rule of thumb, called the rule of 72, is that the doubling time in years is approximately 72 divided by the interest rate \(r\) (as a percentage). For example, at 6% interest, it takes about 12 years to double an investment.
An important concept in business and banking is the time required for an investment to double. A common rule of thumb, called the rule of 72, is that the doubling time in years is approximately 72 divided by the interest rate \(r\) (as a percentage). For example, at 6% interest, it takes about 12 years to double an investment.
- If the interest is compounded continuously at \(r\)%, find the exact doubling time.
- Make a table showing the doubling time in years, for \(r=\) 2%, 4%, 8%, 12%, and 18%, calculated three ways:
- from the exact formula in part a,
- from the rule of 72, and
- from the similar rule of 69.
- Can you think of a reason why people in business would prefer the rule of 72 to the rule of 69?
-
Table P1 contains data on the number of lawyers in a certain town and the total annual income of those lawyers. Assume that during the 5-year period represented by the table, the rate of inflation was 3% per year.Table P1 Lawyers and
their incomeYear No. of Lawyers Total Annual Income 200120\(\$\)2,500,000200223\(\$\)2,700,000200325\(\$\)3,400,000200420\(\$\)3,000,000200525\(\$\)3,600,000- What statistic best describes the financial state of a typical lawyer in a given year? What formula computes it? Construct a table corresponding to this statistic.
-
When were lawyers most well off? Which year saw the greatest improvement? Which year saw the worst deterioration?
-
- Make a table of doubling times for percentage growths from 1% per year to 20% per year.
- What percentage growth rate leads to doubling in years?
- How does your table change if the time unit is a minute instead of a year?
- Suppose a quantity grows at \(n\)% per year for a human lifetime. Explain why the factor by which the quantity grows is about \(2^n\).
\(dP/dt=K P\) with \(P=P_0\) at \(t=t_0\)
has the solution
\(P=P_0 e^{K(t-t_0)}\).

