Exercises

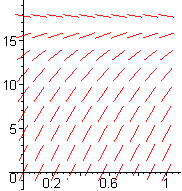
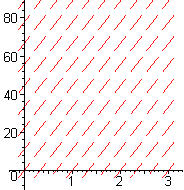
1. Figure E1 shows the slope fields for velocity, according to the Galileo, Stokes, and Velocity-Squared models, not necessarily in that order. Identify which is which.

Figure E1   Raindrop slope fields

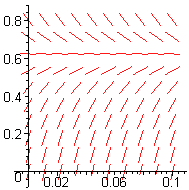Slope Field A	Slope Field B	Slope Field C

• The Galileo Model is represented by Slope Field _____.
• The Stokes Model is represented by Slope Field _____.
• The Velocity Squared Model is represented by Slope Field _____.

2. Recall that a marble dropped from a height of \(535\) feet, according to Galileo's Model (no air resistance), would hit the ground at \(127\) miles per hour. We also computed that a raindrop falling from \(3000\) feet — if it were a marble — would hit the ground at about \(300\) MPH.

   1. Find a formula for the time of fall, according to Galileo's Model, from an arbitrary height \(h\).
   2. Find a formula for the speed at impact in miles per hour. (Be careful with units.)

   You can use the two cases calculated already to check your formula.

   3. Use your formula to find the speed at impact for a fall from \(10\) feet; \(100\) feet; \(1000\) feet; \(10,000\) feet.
3. You have determined the following basic facts for a falling object whose drag (air resistance) is proportional to velocity with proportionality constant \(k\): The terminal velocity \(v\)_term is \(\frac{g}{k}\), and the velocity at time \(t\) is

\(v(t)=v\)_term\(\left(1-e^{-kt}\right)\).

1. Find a formula for the time to reach 99% of terminal velocity, in terms of \(k\).

You may check your formula with the case you already know, the drizzle drop for which \(k=\frac{0.329}{D^2} \times 10^{-5} \text{sec}^{-1}\) and \(D=0.00025\) feet.

2. What would \(k\) have to be in order to take one hour to reach 99% of terminal velocity?
4. Suppose resistance is proportional to \(\sqrt{v}\), as might be the case for a small object falling through a viscous fluid. Find an expression for the terminal velocity in terms of \(g\) and the proportionality constant \(k\).
5. Pilots and parachutists know (and physicists confirm) that the Velocity-Squared Model applies to the resisting force of air on an airplane wing or a falling human body, with or without a parachute. Thus, the acceleration equation has the form \(\frac{dv}{dt}=g-c v^2\). Ms. Jennifer Phillips of Orange, MA, an experienced sky diver, reports the following free fall terminal velocities:

   1. \(170\) mph in fetal position,
   2. \(140\) mph in a nose dive,
   3. \(120\) mph in a horizontal position with arms and legs spread out.

   For each of these cases, find the proportionality constant \(c\).

Note 2 – Sources