Problems

1. Pilots and parachutists know (and physicists confirm) that the Velocity-Squared Model applies to the resisting force of air on an airplane wing or a falling human body, with or without a parachute. Thus, the acceleration equation has the form \(\frac{dv}{dt}=g-c v^2\). Ms. Jennifer Phillips of Orange, MA, an experienced sky diver, reports the following free fall terminal velocities:

   1. \(170\) mph in fetal position,
   2. \(140\) mph in a nose dive,
   3. \(120\) mph in a horizontal position with arms and legs spread out.

   For each of these cases, find the proportionality constant \(c\).

Note 2 – Sources

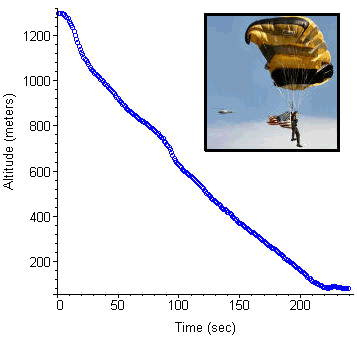
2. The photo inset in Figure P1 shows a member of the US Military Academy's Black Knights Parachute Team jumping from a helicopter into Michie Stadium. The graph in Figure P1 shows the jumper's altitude as a function of time, as recorded by a GPS device carried on the jump.

   Click on Figure P1 to see a movie of the last 90 seconds of the parachute drop. (8.5 MB download)

   Figure P1   Recorded altitudes for a parachute jump

   Note that, after the parachute opens at about 20 seconds, the altitude changes almost linearly, that is, at a constant (terminal) velocity.

   1. Use your Plot tool to fit a line to the "straight" part of the graph, and thereby determine the terminal velocity, both in meters per second and miles per hour.

       

   2. Determine the proportionality constant \(c\) in the Velocity-Squared Model, \(\frac{dv}{dt}=g-c v^2\).

Note 3 – Source and additional information

3. In Figure P2, we zoom in on the first 20 seconds of the parachute jump in Problem 2.

   Figure P2   Recorded altitudes for the start of a parachute jump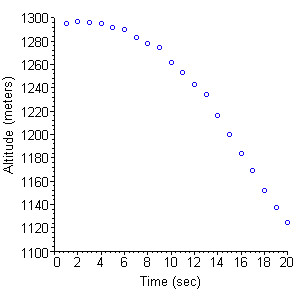

   The chute opened at about 19 seconds, but for several seconds before that, the jumper was falling at terminal velocity for his position with the chute not yet open.

   1. Use your Plot tool to find that pre-parachute terminal velocity.

    

   2. For the brief free-fall period before the parachute opened, determine the proportionality constant \(c\) in the Velocity-Squared Model, \(\frac{dv}{dt}=g-c v^2\).
   3. How does the free-fall terminal velocity compare with the skydiving velocities in Problem 1? Can you explain the differences (if any)?