5.3.6 Derivatives of Sine and Cosine 2: Calculation

To actually calculate the derivative of \(\sin(t)\) we examine algebraically the difference quotient

for small \(\Delta t\). We know from Figure 6 what this expression looks like for varying \(t\) and a particular choice of \(\Delta t\), and you have used this evidence to conjecture what the derivative is. However, there isn't any obvious way to use algebra to verify the conjecture, i.e., to find a factor of \(\Delta t\) in the numerator to cancel with the one in the denominator.

There is, however, a way to make progress with algebra, if we write the numerator in some other form. For this purpose, we recall the trigonometric identity for sine of a sum:

Letting \(\alpha=t\) and \(\beta=\Delta t\), we may write

When we substitute this expression in the numerator of the difference quotient, we obtain

Now we regroup the terms on the right:

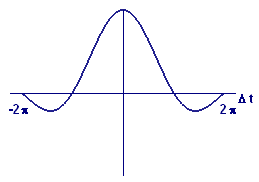
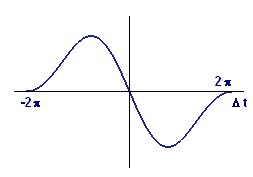
We have now rewritten the difference quotient (left side of the equation) in a form that effectively separates \(t\) from \(\Delta t\). To determine what happens to the difference quotient as \(\Delta t\) shrinks to zero, we only need to find the limiting values of $\frac{\sin (\Delta t)}{\Delta t}$ and $\frac{\cos (\Delta t)-1}{\Delta t}\mathrm{.}$ In Figures 9 and 10, we show graphs of these functions of \(\Delta t\). What do you think the limiting values are as \(\Delta t\) approaches \(0\)?

Activity 6

1. Check your perception by using your calculator to fill in the missing entries in Table 1.

   Table 1   Limiting values for $\frac{\sin (\Delta t)}{\Delta t}$ and $\frac{\cos (\Delta t)-1}{\Delta t}$ as Δ ⁢ t → 0

   Δ ⁢ t	sin ( Δ ⁢ t )	sin ( Δ ⁢ t ) Δ ⁢ t	cos ( Δ ⁢ t ) - 1	cos ( Δ ⁢ t ) - 1 Δ ⁢ t
   1.0	0.84147	0.84147	-0.45970	-0.45970
   0.1	0.099833	0.99833	-0.0049958	-0.049958
   0.01
   0.001
   0.0001
   0.00001

2. What is the limiting value of sin ( Δ ⁢ t ) Δ ⁢ t as Δ ⁢ t approaches \(0\)?

3. What is the limiting value of cos ( Δ ⁢ t ) - 1 Δ ⁢ t as Δ ⁢ t approaches \(0\)?

4. Use your answers to (b) and (c), together with the trigonometric identity

   ${\displaystyle \frac{\sin (t+\Delta t)-\sin \left(t\right)}{\Delta t}=\frac{\sin (\Delta t)}{\Delta t}\cos \left(t\right)+\sin \left(t\right)\frac{\cos (\Delta t)-1}{\Delta t}\mathrm{,}}$

   to show that the derivative of the sine function is what you already knew it had to be.

Comment on Activity 6

We could find the derivative of \(\cos(t)\) in much the same way (see Exercise 10), but it is easier to use what we already know about the derivative of \(\sin(t)\). The two functions are related by this pair of identities:

and

Activity 7

Use the two identities above, your answer to Activity 6, and your other rules for differentiation to find (or confirm) a formula for the derivative of the cosine function.

Comment on Activity 7