Chapter 5
Modeling with Differential Equations
5.5 Trigonometric and Inverse Trigonometric Functions
5.5.1 How Tall is a Tree?
 In Problem 14 of Section 4.5 we proposed a way to find the height of the flame tree pictured at the right. Our physical tools were a mirror and a measuring tape, and our mathematical tool was equality of angles of incidence and reflection. Here we illustrate another way to solve the same problem using a different set of tools. Our physical tools will be a protractor and a measuring tape, and our mathematical tool will be a trigonometric function related to the sine and cosine functions introduced in Section 5.3.
In Problem 14 of Section 4.5 we proposed a way to find the height of the flame tree pictured at the right. Our physical tools were a mirror and a measuring tape, and our mathematical tool was equality of angles of incidence and reflection. Here we illustrate another way to solve the same problem using a different set of tools. Our physical tools will be a protractor and a measuring tape, and our mathematical tool will be a trigonometric function related to the sine and cosine functions introduced in Section 5.3.
Example 1 Find the length of one leg of a right triangle, given the length of the other leg and the measure of the opposite angle. See Figure 1, in which \(\theta\) and \(b\) are the measured quantities, and \(x\) is to be determined.
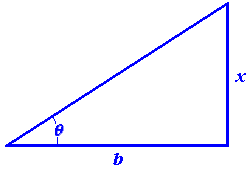
Figure 1 Right triangle
Solution As you no doubt know from a previous course, the ratio \(\frac{x}{b}\) is the tangent of the angle \(\theta\), so \(x=b\,\tan\,\theta\).![]()
 The connection between this calculation and measurement of the tree should be clear. We need to measure a distance away from the base of the tree (using our measuring tape) and then measure an angle formed by sighting to the top of the tree (using our protractor).
The connection between this calculation and measurement of the tree should be clear. We need to measure a distance away from the base of the tree (using our measuring tape) and then measure an angle formed by sighting to the top of the tree (using our protractor).
 |
Activity 1
 Suppose the measurements are as shown in Figure 2: At a distance of \(7\) meters from the base of the tree, the protractor shows an angle of \(61\) degrees to the top of the tree. How tall is the tree?
Suppose the measurements are as shown in Figure 2: At a distance of \(7\) meters from the base of the tree, the protractor shows an angle of \(61\) degrees to the top of the tree. How tall is the tree?- Go outside with a measuring tape and protractor, and measure a tall tree or building.
We stated that the tangent function is related to the sine and cosine functions, and you may remember from your precalculus study what the relationship is. However, nothing about circular or repetitive motion appeared in our discussion of measuring tall objects. The next activity will refresh your memory.
Activity 2
- Referring to Figure 3, express \(\sin\,\theta\), \(\cos \, \theta\), and \(\tan\,\theta\) in terms of \(a\), \(b\), and \(c\).
- Explain why \(\tan\,\theta = \frac{\sin\,\theta}{\cos\,\theta}\).
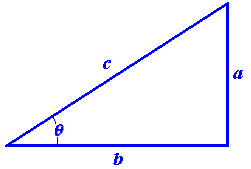
Figure 3 A right triangle
In Example 1 we used the definition of tangent of an angle as "opposite over adjacent", that is, as the ratio of two legs of a right triangle. You may also be familiar with the characterization of tangent as the ratio of sine to cosine. Activity 2 shows that these two ways to characterize the tangent function are equivalent, at least for angles \(\theta\) such that \(0 \leq \theta \leq \frac{\pi}{2}\). But "ratio of sine to cosine" is meaningful for all angles other than those for which \(\cos\,\theta\) is \(0\). Thus, we can draw a graph of the tangent function as a continuous function at all numbers except odd multiples of \(\frac{\pi}{2}\). See Figures 4, 5, and 6.

Figure 4 \(y = \sin \theta\)
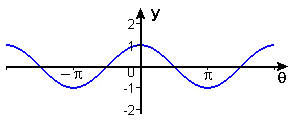
Figure 5 \(y = \cos \theta\)
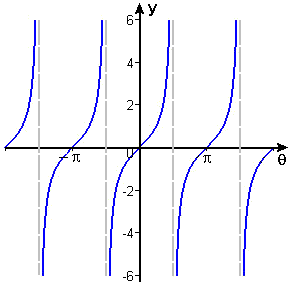
Figure 6 \(y = \tan \theta\)
Note that the tangent function has the value \(0\) at all the places where \(\sin\,\theta=0\), namely at all integer multiples of \(\pi\), and it has a vertical asymptote at all the places where \(\cos\,\theta=0\), namely, at all odd multiples of \(\frac{\pi}{2}\).
Since the sine and cosine are \(2 \pi\)-periodic, the tangent is also \(2 \pi\)-periodic. Explain why the tangent is, in fact, \(\pi\)-periodic.




