Chapter 5
Modeling with Differential Equations
5.5 Trigonometric and Inverse Trigonometric Functions
Problems
-
- Calculate the derivative of \(\sec\theta = \frac{1}{\cos\theta}\).
- Express the answer to part (a) in terms of the functions \(\sec\theta\) and \(\tan\theta\).
- Find the second derivative of \(\sec\theta\).
- Graph \(\sec\theta\) on the interval from \(-2 \pi\) to \(2 \pi\), and match the features of the graph with properties of the function as defined in part (a), as well as properties of the first and second derivatives.
- What is the period of \(\sec\theta\)? Explain.
-
- Calculate the derivative of \(\csc\theta = \frac{1}{\sin\theta}\).
- Express the answer to part (a) in terms of the functions \(\csc\theta\) and \(\cot\theta\).
- Graph \(\csc\theta\) on the interval from \(-2 \pi\) to \(2 \pi\), and match the features of the graph with properties of the function as defined in part (a), as well as properties of the derivative.
- What is the period of \(\csc\theta\)? Explain.
- In Example 3, we determined the optimal distance for placing the museum bench to maximize the vertical viewing angle for a picture on the wall. If Figure 12 were redrawn with that optimal distance, it would look more like Figure P1.
- If you were the designer, would you place the bench this close to the wall? Why or why not?
- Figure P2 repeats Figure 14 showing the vertical viewing angle as a function of distance from the wall. What do you see in this figure to suggest that a different placement might be a better design? Explain.
- Figure P3 shows a right triangle in which \(y\) is the angle whose cosine is \(x\). That is, \(y=\cos^{-1}x\).
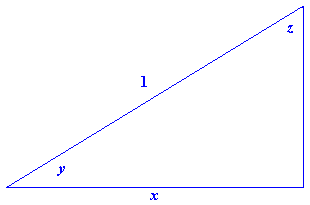
Figure P3 \(y=\cos^{-1}x\)- How is the angle \(z\) related to \(x\)?
- Explain why \(\cos^{-1}x =\frac{\pi}{2}-\sin^{-1}x\).
- What is the derivative of \(\cos^{-1}x\)? (You should be able to answer this with only mental calculation.)
- What is the domain of the inverse cosine function? What is its range?
- Graph both arcsine and arccosine. (The Graph tool will accept either the names asin and acos or arcsin and arccos.)
- What do you think we meant in the Section Summary when we said the inverse cosine "is less interesting and less useful than the inverse sine"?
-
- Explain why \(\cot^{-1}x = \frac{\pi}{2}-\tan^{-1}x\).
- What is the derivative of \(\cot^{-1}x\)? (You should be able to answer this with only mental calculation.)
- What is the domain of the inverse cotangent function? What is its range?
- Graph both arctangent and arccotangent. (The Graph tool will accept either the names atan and acot or arctan and arccot.)
- Figure P4 shows a right triangle in which \(y\) is the angle whose secant is \(x\). That is, \(y=\sec^{-1}x\).
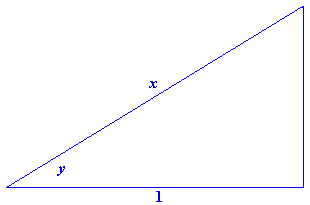
Figure P4 \(y=\sec^{-1}x\)- What is the tangent of the angle \(y\)?
- Use implicit differentiation and the result of Problem 1(a) to find \(\frac{dy}{dx}\). You will need the answer to part (a) to write the result as a function of \(x\).
- What is the domain of the inverse secant function? What is its range?
- Graph both arcsecant and its derivative. Match features of the two graphs. (The Graph tool will accept either the name asec or arcsec. The tool anticipates the answer to part c.)
- Figure P5 shows a right triangle in which \(y\) is the angle whose cosecant is \(x\). That is, \(y=\csc^{-1}x\).
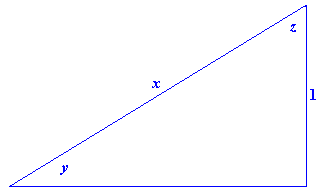
Figure P5 \(y=\csc^{-1}x\)- How is the angle \(z\) related to \(x\)?
- Explain why \(\csc^{-1}x =\frac{\pi}{2}-\sec^{-1}x\).
- What is the derivative of \(\csc^{-1}x\)? (After doing Problem 6, you should be able to answer this with only mental calculation.)
- What is the domain of the inverse cosecant function? What is its range?
- Graph both arcsecant and arccosecant. (The Graph tool will accept either the names asec and acsc or arcsec and arccsc. The tool anticipates the answer to part d.)
 |
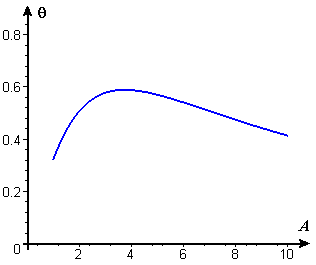 |
Figure P1 Optimal viewing angle |
Figure P2 Viewing angle vs. distance |

