Chapter 5
Modeling with Differential Equations
5.6 Derivative Calculations
5.6.2 Calculations With Algebraic Functions
The class of algebraic functions includes polynomials, rational functions (quotients of polynomials), \(n\)-th roots, and combinations of these functions using the algebraic operations of sum, difference, product, quotient, power, and root.
Find the derivative of the polynomial function \(7x^5-4x^3+2\).
Solution
At this point, you can probably differentiate polynomials in a one-line calculation, as we did here. However, if you need to write down intermediate steps to be confident of your accuracy, please do so. Check carefully to see where we used the Sum Rule, Constant Multiple Rule, and Power Rule.
Calculate \(\frac{d}{du} \sqrt{5u^4-u+1}\).
Solution The first step is to notice that the function to be differentiated is a square root — a \(1/2\)-power — of something. Thus, we combine the Power Rule and the Chain Rule:
The “something” under the square root sign is the polynomial function \(5u^4-u+1\), so the Chain Rule tells us to include a factor that is the derivative of this function. In the second step we calculated that derivative and multiplied the fractions.
In Figure 1 we show the graphs of both \(\sqrt{5u^4-u+1}\) and its derivative, as just calculated. Observe that the derivative is negative where the original function is decreasing, \(0\) when \(\sqrt{5u^4-u+1}\) reaches its minimum, and positive beyond that. This is a simple graphical check of a symbolic calculation — one that you can always carry out with your computer or calculator or with our Graph tool.
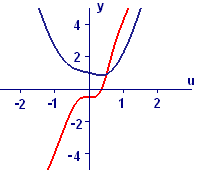
Figure 1 Graphs of \(\sqrt{5u^4-u+1}\) and its derivative



