Chapter 5
Modeling with Differential Equations





5.6 Derivative Calculations

5.6.3 Calculations With Transcendental Functions

A function is said to be “transcendental” if cannot be described by algebraic operations on the independent variable. Logarithms, exponential functions, trigonometric, and inverse trigonometric functions are examples of transcendental functions.

Example 3

Differentiate \(\left[\ln (t)\right]^4\).

Solution

d d ⁢ t [ ln ( t ) ] 4 = 4 [ ln ( t ) ] 3 1 t .

Again we used the Power Rule and the Chain Rule, but this time the derivative-of-the-inside-function factor required the Logarithmic Rule. In Figure 2 we show the graphs of both \(\left[\ln (t)\right]^4\) and its derivative, \(\frac{4\left[\ln (t)\right]^3}{t}\). Again the derivative is negative where the original function is decreasing, \(0\) when \(\left[\ln(t)\right]^4\) reaches its minimum, and positive to the right of the minimum.


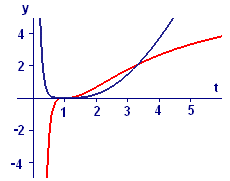
Figure 2   Graphs of \(\left[\ln(t)\right]^4\) and \(\frac{4\left[\ln(t)\right]^3}{t}\)

Checkpoint 3Checkpoint 3

Example 4

Calculate the derivative of \(e^{2t}\cos (3t)\).

Solution

d d ⁢ t [ e 2 t cos ( 3 t ) ] = e 2 t d d ⁢ t cos ( 3 t ) + cos ( 3 t ) d d ⁢ t   e 2 t
  = 3 e 2 t [ - sin ( 3 t ) ] + 2 e 2 t cos ( 3 t )
  = e 2 t [ 2 cos ( 3 t ) - 3 sin ( 3 t ) ] .

The formula for this function, reading from outside in, is a product. Thus the Product Rule comes into play first. That rule in turn calls for a derivative of each factor, so the Cosine and Exponential Rules are used at the second step. But we have cosine of \(3t\) and exponential of \(2t\), so the Chain Rule requires a factor of \(3\) in the first term and a factor of \(2\) in the second term. The final step is an algebraic simplification — not part of the differentiation, but often a good idea for making the result more useful.

Checkpoint 4Checkpoint 4

Checkpoint 5Checkpoint 5

Example 5

Find the derivative of \(\frac{e^{2 \theta}}{cos(3 \theta)}\).

Solution

d d ⁢ θ [ e 2 θ cos ( 3 θ ) ] = d d ⁢ θ [ e 2 ⁢ θ 1 cos ( 3 ⁢ θ ) ]
  = e 2 ⁢ θ d d ⁢ θ [ 1 cos ( 3 ⁢ θ ) ] + d d ⁢ θ ( e 2 ⁢ θ ) 1 cos ( 3 ⁢ θ )
  = e 2 ⁢ θ ( - 1 ) [ cos ( 3 ⁢ θ ) ] - 2 d d ⁢ θ cos ( 3 ⁢ θ ) + 2 e 2 ⁢ θ 1 cos ( 3 ⁢ θ )
  = e 2 ⁢ θ ( - 1 ) [ cos ( 3 ⁢ θ ) ] - 2   3 [ - sin ( 3 ⁢ θ ) ] + 2 e 2 ⁢ θ 1 cos ( 3 ⁢ θ )
  = e 2 ⁢ θ cos ( 3 ⁢ θ ) [ 3 sin ( 3 ⁢ θ ) cos ( 3 ⁢ θ ) + 2 ] .

Checkpoint 6Checkpoint 6

Checkpoint 7Checkpoint 7

Example 6

Find the derivative of \(\left( \sin^{-1}\, t\right)\left(\sin t\right)\).

Solution

Tempting as it might be to think there is some simplifying cancellation here, there is not. We apply the Product Rule to the product of an inverse trig function and a trig function.
d d ⁢ t ⁢ [ sin -1 ( t )   sin ( t ) ] = sin -1 ( t )   ⁢ d d ⁢ t ⁢ ⁢ sin ( t ) +   sin ( t ) ⁢ d d ⁢ t ⁢   sin -1 ( t )  
  = sin -1 ( t )   ⁢ cos ( t ) +   sin ( t ) ⁢   1 1 - t 2 ⁢ .

This strange-looking formula doesn't simplify, but it does reveal that the domain of the derivative function is \(-1 < t < 1\). This is no surprise, since the arcsine graph is vertical at its end points, \(t=\pm 1\).

While the formula looks strange, the derivative function is rather simple, as shown in Figure 3. Note that the original function is even (a product of two odd functions), and its derivative is odd.


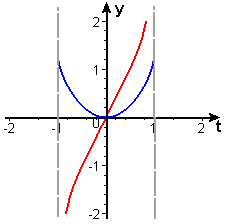
Figure 3   \((\arcsin t)(\sin t)\) (blue) and its derivative (red)

Checkpoint 8Checkpoint 8

Go to Back One Page Go Forward One Page

Go to Contents for Chapter 5Contents for Chapter 5