Problems

1. For each of the following functions,
   1. graph the function,
   2. graph the derivative, and
   3. explain how appropriate properties of the derivative graph confirm your symbolic calculation.
      
      Note: This function grapher expects the independent variable to be be \(t\). Adjust your function definition accordingly.

   \(z=7\ln(3+2t)\)	\(z=\frac{1}{2t+1}\)
   \(y=x^6+4x^2+6x^{-2}\)	\(z=\frac{7}{3+2t}\)
   \(y=2e^{5x}\)	\(y=\frac{\sin 2u}{\cos 5u}\)
   \(y=(\sin 2t) (\cos 5t)\)	\(z=(2t+1)^{12}\)
   \(y=\left(\sin^{-1}\, 2t\right) \left(\cos 5t\right)\)	\(u=\tan^3\, 2x\)

2. For each of the following functions,
   1. graph the function,
   2. graph the derivative, and
   3. explain how appropriate properties of the derivative graph confirm your symbolic calculation.
      
      Note: This function grapher expects the independent variable to be be \(t\). Adjust your function definition accordingly.

   \(y=3\sin t\,\cos 3t\)	\(z=\frac{1}{(2t+1)^2}\)
   \(u=\cos^2\, 3t\)	\(z=\frac{7}{(3+2t)^3}\)
   \(v=\cos(3t^2)\)	\(y=x^7+3x^2+6\)
   \(y=\sin 2t - \cos 5t\)	\(z=2^{5x}\)
   \(y=\tan 2t - \cos 5t\)	\(v=\sin^{-1}\, 5y\)

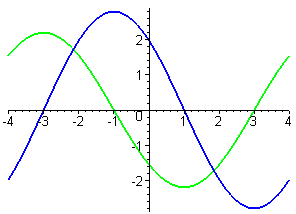
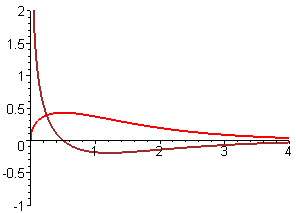
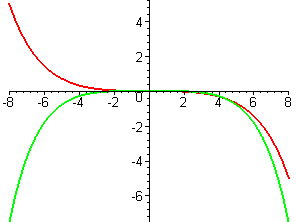
3. In each part of this exercise, graphs of two functions are shown. In each case, one of the functions is the derivative of the other. Decide which function is \(f\) and which is \(f\,'\). Give as many reasons as you can for your choice.
   1. 
   
   
   2. 
   
   
   3. 
   
   
   4.