8.1.2 Moments and Moment Arms

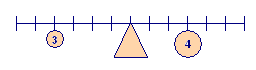
We formulate the discrete center of mass problem in terms of a balance beam - a rigid beam or rod that has negligible mass in comparison with the objects suspended from it. If you experiment with a balance beam, you will discover that different masses on opposite sides of the beam will balance if the products of mass and distance from the balance point are the same, as in Figure 2. For a single mass, this product of mass and distance is called a moment with respect to the balance point, and the distance factor alone is called the moment arm. On the left in Figure 2 we have a mass of three units and a moment arm of four units; on the right, a mass of four units and a moment arm of three units.

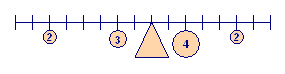
You also may learn from balance beam experiments that moments are additive. Thus, in Figure 3, we can calculate the total moment on the left as \(2 \times 6 + 3 \times 2\) and on the right as \(4 \times 2 + 2 \times 5\). Since each of these moments is \(18\), the beam is balanced.

To make effective use of our information about balancing, in a context involving continuous objects, we need a coordinate system. It is convenient to let the signs of coordinates do the work of keeping track of left and right. Thus we revise our concept of the moment of a point mass to be the product of the mass and its directed distance from the balance axis. Then the condition for balancing is that the sum of the moments is zero.

Checkpoint 1