8.1.3 Center of Mass

In Checkpoint 1 we were able to make the balance point the center of the coordinate system because we already knew that point. Usually we must introduce the coordinate system before we find the balance point - because we will use the coordinates to find the balance point. We can use the balancing condition to locate an unknown center of mass by a simple trick: We create an artificial system consisting of the object of interest on one side of the balance point and a point mass of the same magnitude on the other. Then we are free to place the balance point for this enlarged system where we want it - for example, at the origin of the coordinate system.

We illustrate this idea in Figure 4 with our system of four objects on the right and a single object on the left with mass \(m\) equal to the sum of the masses on the right - in this case \(m=11\) units of mass. We denote the coordinate of the center of mass of the system on the right by \(\bar{x}\). To achieve balance of the enlarged system at \(x=0\), we place the object of mass \(m\) at the symmetrical point on the left, i.e., at \(- \bar{x}\).

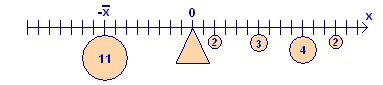
The moment of the system on the right in Figure 4 with respect to the balance point (or, equivalently, with respect to the origin) is unknown, so we just give it a name: \(M\). The moment of the mass on the left is \(- m \bar{x}\). The balancing condition is \(M-m \bar{x} = 0\). Thus we can express the unknown coordinate \(\bar{x}\) in terms of two other unknown quantities, a moment and a mass:

Checkpoint 2

In general, if we have \(n\) objects with masses \(m_1\), \(m_2\), \(...\), \(m_n\) distributed along a balance beam with corresponding \(x\)-coordinates \(x_1\), \(x_2\), \(...\), \(x_n\), the total mass is given by

and the total moment is given by

Then the center of mass is

Checkpoint 3