8.1.4 Calculation of Mass

Now we extend this calculation of center of mass to situations in which the mass is distributed continuously - e.g., to the pool cue. For now we assume that the cue is made of solid wood of uniform density - no added weights.

To find \(\bar{x}\), we need to calculate the moment \(M\) and the mass \(m\). We start with the easier of the two calculations, finding the mass of the pool cue. If we know the volume of the cue and the density of the wood (say, in ounces per cubic inch), then the mass is just the product of the volume and the density. Unfortunately, we do not know the density. However, as we will see, the exact value for the density does not matter in the calculation of the center of mass. For the moment we simply designate this unknown density by \(\delta\) ounces per cubic inch. (The symbol \(\delta\) is the Greek "d," lower-case delta.)

We concentrate now on the calculation of volume. We place the cue along an \(x\)-axis with the butt at the origin and tip at \(58\) (inches), as in Figure 5.

Now that we have a coordinate system, we may determine a function \(r(x)\) that gives the radius of the circular cross section as a function of the \(x\)-coordinate. We know the radius varies linearly, and our diameter measurements of \(9/16\) and \(11/8\) inches give

and

Checkpoint 4

We illustrate the divide-and-conquer process in Figure 6. First, we mentally slice the cue into approximately cylindrical segments and approximate the volumes of these segments by volumes of actual cylinders. Next, we add the volumes of these cylinders to approximate the volume of the cue. Finally, we consider what happens to these sums as the number of terms becomes infinite and the size of each term becomes infinitesimal.

In Figure 6 we have drawn \(31\) cross-sectional cuts at equal intervals. Thus each cross-sectional piece extends along the \(x\)-axis for a distance of \(\Delta x = 58/31 \approx 1.9\) inches. The \(x\)-coordinate of the \(k\)th cut point is

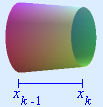
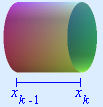
for \(k=0,\,1,\,2,\,...\,,\,31\). We approximate the volume of the \(k\)th section (the one between \(x_{k-1}\) and \(x_k\)) by calculating the volume of the cylinder that has the constant cross-sectional radius \(r(x_{k-1})\). In Figure 7 we show an exaggerated picture of this section of the cue and its cylindrical approximation.

Cue section	Approximation

We obtain the volume of the approximation by the formula for the volume of a cylinder:

Volume = area of base \(\times\) height.

Thus the volume of the cylinder approximating the \(k\)th cue section is

When we add up these cylindrical approximations, we obtain an approximation to the volume of the whole cue:

Volume of the cue ≈ ⁢ ⁢ ∑ k = 1 31 π [ r ( x k - 1 ) ] 2 Δ ⁢ x .

Now there is nothing special about the number \(31\). Suppose we cut the cue into \(n\) sections of equal length. Then the length of each section is

⁢ ⁢ Δ ⁢ x = 58 n inches.

The corresponding cut points are

for \(k = 0,1,...,n\), and the approximate volume of each section is still

Thus the approximate volume of the cue using \(n\) cuts is

As \(n\) increases, these approximations approach the true volume. But we already know that these sums approach the integral

You found the formula for the function \(r(x)\) in Checkpoint 4.

Checkpoint 5

The volume of the cue is the value of this integral, approximately \(45.4\) cubic inches, so the mass of the cue is approximately \(45.4 \, \delta\) ounces.