Problems

1. Explain why the beam is balanced in Figure P1.

   
   Figure P1   A balanced beam

2.    Figure P2   Office mobile

   Figure P2 shows an amateur mobile (office art) made from string, pencils, and Liquid Paper bottles. Explain how you can tell that the bottles are not all full and not all empty.
3. Find the center of mass of a 65-inch-long tapered rod that has a diameter of 0.75 inch at the larger end and a diameter of 0.25 inch at the smaller end.
4. Find the center of mass of a 60-inch-long tapered rod that has a diameter of 0.70 inch at the larger end and a diameter of 0.15 inch at the smaller end.
5. Use an integral to explain the formula \(V=\frac{1}{3} \pi R^2 h\) for the volume of a circular cone of radius \(R\) at the base and height \(h\).
6. Find the \(y\)-coordinate of the center of mass of the cone in Figure P3.

   
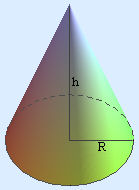
   Figure P3   A circular cone of radius \(R\) and height \(h\)

7. The horn-shaped object in Figure P4 has circular cross sections. The radius \(r\) varies with \(x\) according to the formula

   \(r(x)=\frac{1}{2} x^2\) for \(0 \leq x \leq 1\).

   Find the volume of the horn.

   
   Figure P4   A parabolic horn

8. The horn-shaped object in Figure P5 has circular cross sections. The radius \(r\) varies with \(x\) according to the formula

   \(r(x)=\frac{1}{2} + x^2\) for \(0 \leq x \leq 1\).

   Find the volume of the horn.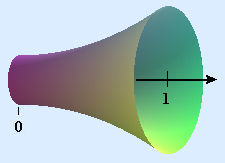

   
   Figure P5   Another parabolic horn

9. The horn-shaped object in Figure P6 has circular cross sections. The radius \(r\) varies with \(x\) according to the formula

   \(r(x)=\frac{1}{2} + \frac{1}{2} e^x\) for \(0 \leq x \leq 1\).

   Find the volume of the horn.

   
   Figure P6   An exponential horn

10. A cylindrical rod with diameter 10 centimeters and length 75 centimeters has a variable density. If we place the rod in a coordinate system as indicated in Figure P7, the density has the form

    \(\delta (x) =0.01+0.0001 x\)

    grams per cubic centimeter.

    
    Figure P7   A cylindrical rod

    1. Find the mass of the rod.
    2. Find the center of mass of the rod.
11. A thin cylindrical rod with diameter 5 centimeters and length 90 centimeters has a variable density. If we place the rod in a coordinate system as indicated in Figure P8, the density has the form

    \(\delta (x) =0.005+0.0002 x\)

    grams per cubic centimeter.

    
    Figure P8   A cylindrical rod

    1. Find the mass of the rod.
    2. Find the center of mass of the rod.