8.2.1 An Aircraft Mobile

In the preceding section we considered the problem of finding the center of mass of objects that, because of their symmetry, were essentially one-dimensional. For the pool cue, the only significant question was where the center of mass was located along its length.

The most important center-of-mass problems are three-dimensional. For example, the designer of an aircraft has to know where its center of mass will be - under all allowed loading conditions - in order to make sure that it is over the wings. Otherwise the plane won't fly. Furthermore, the center of mass has to be a little forward of the main landing gear; too far back, and the tail will drag on the runway. In Figure 1 we show an aircraft with rear fuselage-mounted engines. Aircraft with wing-mounted engines have the wings and landing gear farther forward - engines are heavy.

The problem of finding the center of mass in an object as complicated as a real aircraft is still beyond our capabilities, so we will simplify the problem to one of two dimensions. Suppose you draw Figure 1 on a cardboard cutout of the same shape and hang it from a thread - for example, as part of a mobile displaying types of research aircraft. Where would you place the thread?

Try this at home: If you can send a file to a printer, click here for a printable copy of Figure 1 from which you can make your own aircraft mobile.

Our problem is now simplified to one of finding the center of mass of a piece of cardboard in the shape shown in Figure 2.

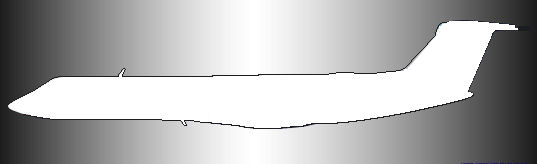
We'll assume that the cardboard has thickness \(\theta\) (the Greek "th," lower-case theta) inches and a density \(\delta\) ounces per cubic inch. We will see that we do not need to know the actual values of these two constants. The center of mass of a two-dimensional figure has two coordinates, \(\bar{x}\) and \(\bar{y}\). To find these, we need to find the mass and the moments in both horizontal and vertical directions. We will take this a step at a time.