Problems

1. 1. Find the center of mass of the plane region bounded by the line \(y=x\), the \(x\)-axis, and the line \(x=1\). (Can you do this without evaluating any integrals?)
   2. Find the center of mass of the region bounded by the curve \(y=x^2\), the \(x\)–axis, and the line \(x=1\).
   3. Find the center of mass of the region bounded by the curve \(y=x^3\), the \(x\)–axis, and the line \(x=1\).
   4. Find the center of mass of the region bounded by the curve \(y=x^n\), the \(x\)–axis, and the line \(x=1\), where \(n\) is a positive integer.
   5. If we denote the center of mass in part (d) by \(\left(\bar{x}_n,\bar{y}_n\right)\), what do you think the limiting values of \(\bar{x}_n\) and \(\bar{y}_n\) are as \(n\) becomes infinitely large? Calculate the limiting values from your answer to part (d). Do you find anything surprising in your results?
2. The photo at the right shows a famous sculpture by Alexander Calder, the massive mobile/stabile Mountains and Clouds, which was designed for the atrium of the Hart Senate Office Building in Washington, DC. Our focus in this exercise is on the mobile part of the sculpture, the four "clouds," which are suspended in roughly horizontal planes.
   
   

   1. Explain why only the two lowest clouds have to be suspended from their centers of mass. (Finding suspension points for the two upper clouds is beyond our present capabilities.)

   The lowest cloud on the left is roughly a quarter-circle, so you may already have found its center of mass in Exercise 3. We concentrate now on the lowest cloud on the right, whose approximate shape is shown in Figure P1. The units in the figure are arbitrary and are chosen for convenience in drawing. The bounding lines and curves are \(y=6-x\), \(y=6+x\), \(y=\frac{x(6-x)}{18}\), and \(y=-\frac{x(6-x)}{18}\). By symmetry, \(\bar{x}=0\), so our problem is to find \(\bar{y}\).

   
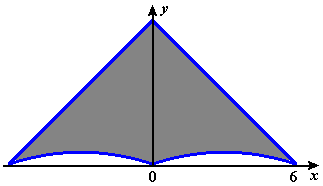
   Figure P1   A Calder cloud
   
   
   2. Suppose the cloud shape were triangular, i.e., without the curved cutouts at the bottom of Figure P1. Where would the center of mass be located? (You may answer this question using either geometry or calculus. Your answer will serve as a check, because the cutouts should not move the center of mass very much.)
   3. Find \(\bar{y}\). (Hint: Your integrals will be over the interval \([-6,6]\), but you will need to integrate separately from \(-6\) to \(0\) and from \(0\) to \(6\) because the formulas for the functions change.)

3. Figure P2   Cutout for a mobile

   You are making a mobile, and one of the suspended parts is to have the shape shown in Figure P2. If the origin of the coordinate system is placed at the nose of the figure, the upper half of the figure is bounded by the graphs of \(y=\sqrt{x}\), \(y=x-2\), and \(x=7\). You are going to cut the shape from a sheet of a thin material. At what point will you attach the thread so that the figure will hang in a horizontal plane?