Chapter 8
Integral Calculus and Its Uses
8.3 Numerical Approximation of Integrals
We have seen a variety of reasons for wanting to calculate definite integrals - to find distances, areas, volumes, and centers of mass. In future sections we will see many more. Thus we need to be able to calculate these integrals with confidence. One way of performing these calculations is close at hand: your computer algebra system. You enter the function and the limits, and it does the rest, returning a numerical approximation to the integral. How does it do that?
In this section we explore numerical procedures for calculating definite integrals, procedures that are not difficult, just tedious. Your computer uses procedures like these to calculate the numerical approximations. These procedures are effective tools for rapid enough calculation that we can generate numerical or graphical antiderivatives, even when we can't find formulas for them.
8.3.1 Left-Hand and Right-Hand Sums
Our starting point is the definition of the definite integral in terms of sums of products. Specifically, we formed the sum
to calculate the sum of areas of rectangles with height \(f(t_{k-1})\) and width \(\Delta t\), where \(\Delta t\) is the width of each subinterval when the interval \([a,b]\) is divided into \(n\) equal pieces. Then we defined the integral of \(f\) from \(a\) to \(b\) to be the limiting value of such sums as \(n \rightarrow \infty\) and \(\Delta t \rightarrow 0\). It follows that for large values of \(n\), the sum should itself be a good approximation to the limiting value, i.e., to the integral.
The function values in this sum are calculated at the left-hand endpoints of the subintervals - i.e., at \(t_{k-1}\) for the \(k\)th subinterval \([t_{k-1},t_k]\). For this reason, we call this sum a left-hand sum. Similarly, we can calculate a right-hand sum by using function values at the right-hand end of each subinterval.
| Definitions If \(f\) is continuous on the interval \([a,b]\), \(n\) is a positive integer, and \(\Delta t = \frac{b-a}{n}\), then
is the corresponding left-hand sum approximation to the integral The sum is the corresponding right-hand sum approximation to the same integral. |
We illustrate right- and left-hand sums by recalling a calculation from Chapter 7. There we estimated the distance traveled during a short automobile trip by integrating the velocity function over the time interval from \(0\) to \(13\) minutes. Thus we wanted the value of the definite integral
where \(v(t)\) is the function graphed in Figure 1 and tabulated in Table 1, both repeated from Chapter 7.
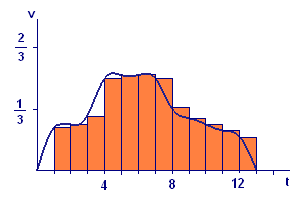
| Time | Speed (miles/min) | Time | Speed (miles/min) |
0 |
0 |
7 |
0.500 |
1 |
0.233 |
8 |
0.333 |
2 |
0.250 |
9 |
0.283 |
3 |
0.303 |
10 |
0.250 |
4 |
0.500 |
11 |
0.217 |
5 |
0.517 |
12 |
0.183 |
6 |
0.517 |
13 |
0 |
Find the left-hand sum approximation for \(n=13\) and \(\Delta t=1\) to
Solution Since \(\Delta t = 1\) we need only add up the first \(13\) function values. The left-hand sum is \(4.086\)![]() .
.
We saw in Section 7.1 that we could refine our estimate of the area under the curve in Figure 1 (i.e., the integral) by calculating left-hand sums with large numbers of terms. We turn now to an example for which we can compare sums to a known exact value for an integral - unlike the velocity example, for which we had no formula. Our purpose in estimating an answer we already know is to get some sense of how many terms are needed to achieve a given accuracy.
In Figure 2 we show the graph of \(y=1/x\), under which we have shaded the area from \(x=1\) to \(x=3\).
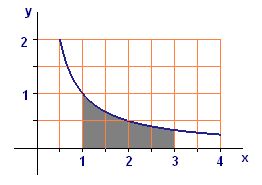
According to the Fundamental Theorem, the shaded area in Figure 2 is
We have given the answer to \(15\) decimal places because we need a highly accurate answer to compare to our approximations.
Activity 1
The \(10\)-term left-hand sum approximating the area in Figure 2 starts out
.Fill in the other seven terms, and calculate the sum.
Calculate the right-hand sum with ten terms.
-
Subtract the known area \(\ln (3)\) from the left-hand sum in part (a) and the right-hand sum in part (b) to find the errors in these two approximations.
Explain the signs of the errors by referring to Figure 2.
In Table 2 we show the results of calculating \(10\)-term, \(100\)-term, and \(1000\)-term left-hand sums and right-hand sums approximating the shaded area in Figure 2. In the last two columns of the table we show the errors in these approximations, obtained by subtracting the \(15\)-place value of \(\ln (3)\). The \(n=10\) row in the table should confirm what you just did in Activity 1.
Activity 2
How do the errors in left-hand sum and right-hand sums compare in size?
What happens to the error in LHS when the number \(n\) of subdivisions is made \(10\) times larger? In RHS?
Activity 3
Explain why, if \(f\) is any decreasing function, then any LHS will overestimate the integral and any RHS will underestimate the integral.
What can you conclude if \(f\) is an increasing function? Explain your answer.
Activity 4
Explain why LHS and RHS can be written in the following way:
Subtract the LHS equation from the RHS equation, and make appropriate cancellations and substitutions to show that
-
Explain why the calculation in part b implies that errors should decrease by a factor of \(1/10\) each time \(n\) is increased by a factor of \(10\).
![]() Animation We have argued both numerically and algebraically that the LHS and RHS get close to each other and to the integral for large values of \(n\). The pop-up animation illustrates this geometrically. In order to have enough steps to see the progression, we double \(n\) at each step instead of multiplying by \(10\). With over \(100\) steps, you can see that LHS and RHS are almost the same, but you can still see slight differences at screen resolution.
Animation We have argued both numerically and algebraically that the LHS and RHS get close to each other and to the integral for large values of \(n\). The pop-up animation illustrates this geometrically. In order to have enough steps to see the progression, we double \(n\) at each step instead of multiplying by \(10\). With over \(100\) steps, you can see that LHS and RHS are almost the same, but you can still see slight differences at screen resolution.
We've just run up against a reality check. It looked like we were making good progress on the problem of finding accurate approximations to integrals - all we have to do to decrease the error by a factor of \(1/10\) (i.e., gain accuracy to one more place) is multiply the number of steps by \(10\). But to achieve even moderately good accuracy, this may require sums with millions of terms! That's simply not practical. We need a better idea.



