8.5.2 Using Integrals to Analyze Waveforms

We consider now the harder inverse problem: If you have a complicated periodic function, how can you break it down into simple trigonometric terms? We begin our attack on this problem with investigation of certain definite integrals of trigonometric functions over complete periods. Then we will see how this information about integrals can be used to solve a simplified version of the inverse problem. In exercises or a project associated with this chapter you may solve a more substantial problem.

Activity 1

1. Calculate each of the following integrals:

   ⁢ ∫ - π π 1 d t , ⁢      ⁢ ∫ - π π sin ⁢ t d t , ⁢      ⁢ ∫ - π π cos ⁢ t d t , ⁢      ⁢ ∫ - π π cos ⁢ 2 t d t . ⁢

2. Use a graph of each of the integrands to explain why each of the integrals has the value you just calculated.

3. Make a conjecture about the values of the integrals

   ⁢ ∫ - π π sin ⁢ n ⁢ t d t ⁢    and    ⁢ ∫ - π π cos ⁢ n ⁢ t d t , ⁢

   where \(n\) is any positive integer.

4. Verify your conjecture by calculating the integrals in part (c).

Comment on Activity 1

Now we consider integrals of products of these basic functions.

Activity 2

1. Figure 3 shows the graph of

   y = cos ⁢ t ⁢ cos ⁢ 2 t

   on the interval from \(- \pi\) to \(\pi\). Guess the value of

   y = ∫ - π π cos ⁢ t ⁢ cos ⁢ 2 t d t

   from the graph. Explain your guess.

   
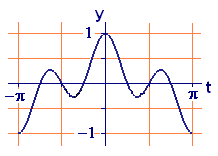   Figure 3   Graph of \(y = \cos\,t\,\cos\,2t\)

2. Use the Definite Integral tool to evaluate the integral in part (a).

3. Assume that \(n\) and \(m\) are nonzero integers. Use the Definite Integral tool to evaluate each of the following integrals. You can use \(n\) and \(m\) in the function definitions.

   \(\displaystyle \int_{-\pi}^{\,\pi} \cos\,nt\,\cos\,mt \,dt\) (for \(n \neq m\))

   \(\displaystyle \int_{- \pi}^{\,\pi} \sin\,nt\,\sin\,mt \,dt\) (for \(n \neq m\))

   \(\displaystyle \int_{- \pi}^{\,\pi} \cos\,nt\,\sin\,mt \,dt\)

   In the first two cases, you will have to interpret the answers, because the tool does not know that \(n\) and \(m\) are integers or that they are distinct. (Notice that there is no restriction that \(n \neq m\) for the last integral.)

Comment on Activity 2

The only integrals of products of basic trigonometric functions we have not examined yet are integrals of squares, \(\cos^2\,nt\) and \(\sin^2\,nt\) — that is, the cases where \(n\) and \(m\) are equal. We take these up in the next activity.

Activity 3

1. Figure 4 shows the graph of \(y = \cos^2\,t\) from \(- \pi\) to \(\pi\). Use the graph to explain why

   ∫ - π π cos 2 ⁢ t d t

   cannot be zero.

   
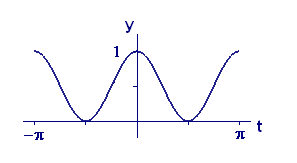   Figure 4   Graph of \(y = \cos^2\,t\)

2. Use the trigonometric identity

   cos 2 ⁢ t = 1 + cos ⁢ 2 t 2

   to calculate

   ∫ - π π cos 2 ⁢ t d t .

3. Assume that \(n\) is a nonzero integer, and calculate

   ∫ - π π cos 2 ⁢ n ⁢ t d t .

4. Assume that \(n\) is a nonzero integer, and calculate

   ∫ - π π sin 2 ⁢ n ⁢ t d t .

[Recall that \(\sin^2\,t = \frac{1-\cos\,2t}{2}\).]

Comment on Activity 3

Here is the central puzzle of this section: In Figure 5 we show the graph of a function \(f(t)\) that has the form \(f(t)=b_0+b_1\,\cos\,t+b_2\,\cos\,2t\) for some choice of the constants \(b_0\), \(b_1\), and \(b_2\). Suppose we can calculate numerical values of the function \(f\) but we do not know the formula, i.e., the values of the constants \(b_0\), \(b_1\), and \(b_2\). How can we determine the values of the constants?

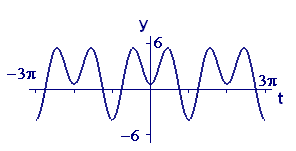
In a more realistic setting, such as the EKG in Figure 1, there is a way to get numerical values of the periodic function - read them from the graph - even though there is no formula in sight. Since the EKG appears to combine several different repeating phenomena, we might suspect that a good fit by a formula would require both sine and cosine terms of many different frequencies. The observations we shall make here about finding the coefficients would apply to that case as well. That is, the simple case illustrated in Figure 5 contains all the complexities required for dealing with more realistic problems.

Activity 4

1. Use the form of the unknown function \(f(t)\) to write an expression for

   ∫ - π π f ( t ) d t

   in terms of integrals of the elementary functions \(1\), \(\cos\,t\), and \(\cos\,2t\). Then use this expression and the results of Activity 1 to show that

   b 0 = 1 2 π ∫ - π π f ( t ) d t .

2. Multiply both sides of the equation for \(f(t)\) by an appropriate trigonometric function to find an expression for

   ∫ - π π f ( t ) cos ⁢ t d t .

   Use this expression and the results of Activities 1, 2, and 3 to find a formula for \(b_1\).

3. Now multiply both sides of the equation for \(f\) by an appropriate trigonometric function to find an expression for

   ∫ - π π f ( t ) cos ⁢ 2 t d t .

   Use this expression and the results of Activities 1, 2, and 3 to find a formula for \(b_2\).

Comment on Activity 4

Checkpoint 1