Chapter 8
Integral Calculus and Its Uses
8.5 Representations of Periodic Functions
In Figure 1 we show an important periodic (or repeating) function: a trace from an electrocardiogram (EKG) of one of the authors. An EKG measures various aspects of the functioning of the heart. Each of us finds it important that the heart do essentially the same thing over and over, roughly once a second, for a large number of years. When the heart is not doing that, the EKG is a first-line diagnostic tool for discovering and interpreting deviations from regular behavior.

We first brought up the subject of repeating phenomena in Chapter 5, where we mentioned some other examples, such as the motion of planets and pendulums. To these we might add musical tones and other sounds, daily and yearly temperature fluctuations, light rays, and water waves. The central point was the observation of the role of trigonometric functions in representing these phenomena. That's the point we return to now.
8.5.1 Building Complicated Waveforms from Sines and Cosines
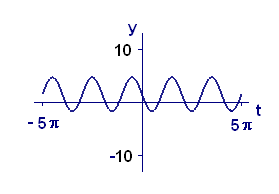
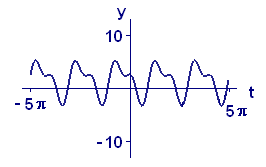
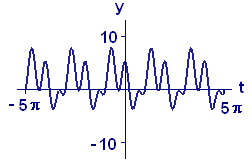
One way to analyze periodic functions is to try to break them down into simpler components. The reason this might work is that quite complicated periodic functions can be built up out of the elementary periodic functions: \(\sin\,t\), \(\sin\,2t\), \(\sin\,3t\), \(...\), and so on, together with \(1\), \(\cos\,t\), \(\cos\,2t\), \(\cos\,3t\), \(...\), and so on. (The constant function \(1\) can be thought of as \(\cos\,0t\)). For example, consider the sequence of functions whose graphs are shown in Figure 2. When we add terms that oscillate twice as fast and three times as fast as the earlier terms, the resulting functions became considerably more interesting. If we continued to add terms that oscillate even faster, such as \(\cos\,4t\) or \(\sin\,7t\), we could produce even more complicated graphs.
 |
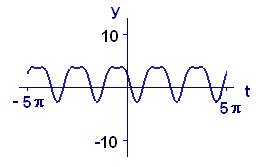 |
| \(f(t)=1.53-3.19\,\sin\,t\) | \(f(t)=1.53-3.19\,\sin\,t+1.07\,\cos\,2t\) |
 |
 |
| \(f(t)=1.53-3.19\,\sin\,t\) \(+1.07\,\cos\,2t+1.45\,\sin\,2t\) |
\(f(t)=1.53-3.19\,\sin\,t+1.07\,\cos\,2t\) \(+1.45\,\sin\,2t+ 2.73\,\cos\,3t\) |

