Chapter 5
Modeling with Differential Equations





5.4 Modeling With Circular Functions

5.4.1 How Much Daylight?

Before we use sines and cosines to solve the spring-mass problem, we examine the behavior of somewhat more complicated sine functions. We will apply these functions to another modeling problem, one that does not involve a differential equation.

Activity 1

Use the Sine Functions tool to explore functions of the form

f ( t ) = A + B   sin ( C ( t - D ) ) .

  1. How does varying \(A\) affect the graph of \(f\)?

  2. How does varying \(B\) through positive values affect the graph of \(f\)?

  3. What is the effect of changing the sign of \(B\)?

  4. How does varying \(D\) affect the graph of \(f\)?

  5. How does varying \(C\) through positive values affect the graph of \(f\)?

Comment 1Comment on Activity 1

Cyclical phenomena abound in nature. We look first at the seasonal variation in the hours of daylight at Frederick, MD in 2006. We will start with sunrise and sunset data (EST) for Frederick from the U. S. Naval Observatory.

In Figure 1 we graph the monthly averages for the number of minutes after midnight for both sunrise and sunset at Frederick. In Figure 2 we show the average number of minutes of daylight -- time of sunset minus time of sunrise. This is an example of subtraction of one data-defined function from another, similar to the Canadian trade balance example in Section 1.5.

Figure 1   Average monthly sunrise and sunset in Frederick, MD

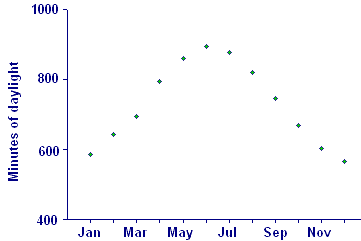Figure 2   Minutes of daylight in Frederick, MD

Activity 2

Use our Fit Daylight Data tool to fit a function of the form

f ( t ) = A + B   sin ( C ( t - D ) )

to the minutes of daylight values displayed in Figure 2.

Comment 2Comment on Activity 2

Checkpoint 1Checkpoint 1

Image credit
Go to Back One Page Go Forward One Page

Go to Contents for Chapter 5Contents for Chapter 5