Chapter 5
Modeling with Differential Equations
5.4 Modeling With Circular Functions
5.4.2 Euler's Method Solutions for the Spring Equation
Our investigation of spring motion in Section 5.3 led us to the differential equation of motion,
where \(x\) is the vertical displacement of the spring, \(m\) is the mass of the spring bob, \(k\) is the spring constant, and \(t\) is time.
If we formulate our problem as an initial value problem, then we have some hope that we can generate a numerical or graphical solution, which may in turn provide some evidence about the role to be played by sine and cosine functions.
In addition to the equation of motion, we know something about how the motion starts. In particular, if we pull the mass to an initial displacement \(x_0\) before we let go, then we know that \(x(0)=x_0\). And if we simply let go, that is, if we don't throw the mass either up or down, then the initial velocity, \(x'(0)\), must be zero. Thus, we can state our initial value problem — after solving for the second derivative — in the following way:
Euler's Method, as we have used it so far, seems to apply only to first-order equations, that is, to equations in which the first derivative is expressed by a formula involving the independent or dependent variables. However, it works just as well for a pair of first-order equations. What we need to do is write the single second-order differential equation as a pair of first-order equations.
Where should we look for the second unknown function for the second equation? In fact, we have two strong hints in our previous work about where to look. First, we already have two initial conditions, one for the function \(x\) we are trying to find, the other for its derivative \(x'\). Perhaps the second function should be the velocity! That would fit with the second hint, which comes from the falling body problem, in which our actual approach to solving the equation \(s''(t)=g\) was to solve two first-order problems, one for finding velocity from acceleration, the other for finding position from velocity.
Suppose \(x(t)\) is the desired function for the position of the bouncing mass at time \(t\), i.e., the solution of the initial value problem. If we write \(v(t)=x'(t)\), then \(x\) and \(v\) must satisfy the system of first-order equations
and
with the initial conditions
and
Be sure you know where each of these four equations comes from.
Recall the basic idea of Euler's Method: We step forward in time in steps of equal length \(\Delta t\), so \(t_0=0\), \(t_1=\Delta t\), \(t_2=2(\Delta t)\), and so on. Initially, we know starting values for \(x\) and \(v\) from \(x(0)=x_0\) and \(v(0)=0\), and we can calculate starting slopes for the two functions by substituting these values in \(x'=v\) and \(v'=-(k/m)x\). Given slopes, we can calculate a rise for each function as slope\(\times\)run. Adding each rise to the corresponding starting value gives the next value for each function. And then we start over: From known function values, we use the differential equations to calculate slopes, use slopes to calculate rises, and add rises to find the next values.
Of course, the rises we are calculating are really \(dx\) and \(dv\) — rises to tangent lines — instead of what we really want to know, \(\Delta x\) and \(\Delta v\) — rises to the unknown curves. Euler's Method is only as good as the approximations \(dx \approx \Delta x\) and \(dv \approx \Delta v\). (See Section 5.2.)
The discussion in the last two paragraphs leads to the following forward-stepping formulas:
with
| \(x_0=\) the starting displacement |
| \(v_0=0\). |
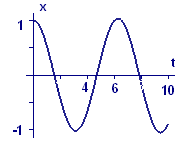
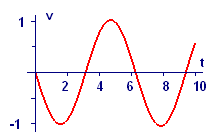
In Figures 4 and 5 we show solutions for \(x\) and \(v\) generated from these formulas for a starting displacement \(x_0\) of one unit and \(k/m=1\).
 |
 |
|
Figure 4 Numerical solution for position \(x(t)\) of the mass bouncing on the spring |
Figure 5 Numerical solution for velocity \(v(t)\) of the mass bouncing on the spring |
Activity 3
Examine Figures 4 and 5 carefully. Do the curves behave the way you would expect from what you know about the physics of the spring-mass system?
Are the curves believable as a solution to the initial value problem
\(\frac{dx}{dt}=v\) with \(x(0)=1\), \(\frac{dv}{dt}=-x\) with \(v(0)=0\)? Why or why not?
-
How do you think the numerically generated graphs of \(x=x(t)\) and \(v=v(t)\) are related to the sine and/or cosine functions? Does the relationship fit with what you know about derivatives of these functions?



