8.2.2 Calculation of Mass

First, we need to calculate the mass \(m\) of the cutout. As before, this is just density \(\times\) volume, and since the thickness is constant, the volume is area \(\times\) thickness. Thus,

So the calculation of the mass \(m\) is reduced to the calculation of the area.

We can determine the area by our divide-and-conquer strategy. First, we slice the shape into approximately rectangular segments. Then we approximate the areas of these segments by areas of actual rectangles. Finally, we consider what happens to the sum of the rectangular areas as the number of terms becomes infinite and the size of each term becomes infinitesimal.

Checkpoint 1

Notice that part (a) of the checkpoint task is much easier with \(18\) strips (the number shown) than it would be if we had subdivided into only \(2\) or \(3\) strips. As the number of strips increases, each strip looks more like a rectangle, regardless of the shape of the original object. If we drew the figure with \(180\) strips, it would be tedious to draw all those rectangles, but it would be easy to decide where to draw the top and bottom of each strip.

After you have drawn your own rectangular approximation to the airplane shape, look at our solution in Figure 3, in which we have also added coordinate axes. It is not important that your rectangles match ours exactly or that your estimate of area based on strips agree exactly with ours. We can only imagine the process of letting the number of strips become infinite, but as it does, our differences in estimation will disappear.

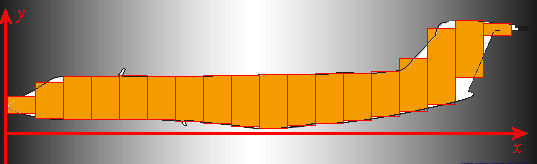
Let's call the points of subdivision on the \(x\)-axis \(x_0,\,x_1,\,x_2\), and so on, up to \(x_{18}\). (In this case, \(x_0=0\) because of our placement of the origin.) As before, we write \(\Delta x\) for the constant spacing between the points; thus \(\Delta x = x_k - x_{k-1}\) for every \(k\) from \(1\) to \(18\). The spacing between points on the \(x\)-axis is also the width of each of our rectangles, one of the things we need to know in order to calculate area. Now suppose that we know a function \(h\) whose value at \(x\) is the vertical distance (height) across our cutout at that particular \(x\). Then the height of the \(k\)th rectangle is approximately \(h(x_k)\). Thus the total area is approximately

This time we have written the approximation as a right-hand sum, i.e., we approximated by assuming that \(h\) has the constant value \(h(x_k)\) on the interval \([x_{k-1},x_k]\). In our previous applications of the divide-and-conquer process we used only left-hand sums. We will see in the next section that it doesn't make much difference - if the number \(n\) of subdivisions is sufficiently large, the left- and right-hand sums are very close to each other and to the actual area. Furthermore, as \(n\) becomes large, not only do all the area-approximating sums get closer to the actual area, but also they get closer to the definite integral of \(h\) from one end of the airplane cutout to the other. Thus the area of the cutout must be that integral.

That's as far as we can take the explicit calculation right now, since we don't have a formula for the function \(h\), and therefore, we have no way to actually evaluate the integral. However, we have made the following progress on a procedure for calculating a center of mass. To find the mass of a planar shape of uniform density and thickness:

• Find the area of the shape as

  A = ∫ a b h ( x ) d x ,

  where \(h\) is the function giving vertical height at any \(x\), and \(a\) and \(b\) are the endpoints of the interval over which the shape extends.

• Calculate the mass as \(m = \delta \theta A\), where \(\delta\) is the density, and \(\theta\) is the thickness.

Checkpoint 2