8.6.1 Why Not Let the Computer Do It?

In contrast to antidifferentiation, differentiation is easy! Just follow the rules — to the letter — and the right answer is automatic. The procedure is so straightforward that machines can and do carry it out. Many calculator and computer programs can differentiate virtually any function that can be defined by a formula, and they almost always get the right answer. Often humans don't get the right answer, but that's because it is sometimes difficult to keep track of and follow all the algebraic rules correctly — not because there is anything tricky or mysterious about the procedure.

Integration is another matter altogether. Undoing differentiation often requires great ingenuity to find just the right combination of algebraic maneuvers, and for many problems there may be a lot of trial and error before that combination is found. Indeed, given a formula for a function that is the derivative of something, it is often not clear whether the something can be defined by a formula in the usual sense.

Some computer programs — those called computer algebra systems (CAS) — can find indefinite integrals (antiderivatives) as well as derivatives. However, you may have already discovered that our CAS, Sage, will occasionally fail to find an integral that you know — or strongly suspect — does have a formula. You may need some algebraic strategies for working in partnership with Sage to achieve success in these cases. In this section we will offer some examples and activities to reinforce this concept of human and computer algebra working together.

Before we begin our exploration of the use of CAS for integration, recall that two rather different types of problems have led us to a need for evaluating indefinite integrals. First, almost from the beginning of this course we have been concerned with the problem of solving differential equations, and we saw in Chapter 6 that this problem often can be turned into one of indefinite integration (although this term was not introduced until Chapter 7). Second, our study in Chapter 7 of the divide-and-conquer technique and the Fundamental Theorem has shown us that indefinite integrals can be used as a tool for evaluating definite integrals. We note in passing that every CAS can evaluate a definite integral of an explicit function with explicit limits of integration (i.e., with specific values for all of the constants involved), but in the preceding section we saw a need for evaluating definite integrals of functions with parameters (constants with names but unspecified values) in order to find Fourier coefficients.

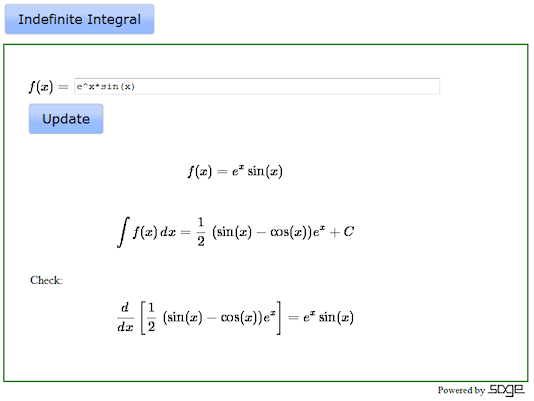
The image below (not an actual Sage interact) shows how a Sage tool integrates the function \(f(x)=e^x \sin(x)\) and then differentiates the result to confirm that the integration did in fact produce an antiderivative. This is a useful checking step to keep in mind whenever using a computer or calculator to do indefinite integration. We will use this tool at appropriate places in this section.