Problems

1. Assume \(f\) is a function of the form

   \(\displaystyle f(t)=b_0+a_1\,\sin\,t+b_1 \,\cos\,t+a_2\,\sin\,2t\).

   1. Find \(\displaystyle \int_{-\pi}^{\,\pi}\,f(t)\,\sin \,3t\,dt\).
   2. Find \(\displaystyle \int_0^{\,\pi}\,f(t)\,dt\).
      
      
   3. Find a formula for \(f\) if

      \(\displaystyle \int_{-\pi}^{\,\pi}\, f(t)\,dt=2\), \(\displaystyle \int_{-\pi}^{\,\pi}\,f(t)\,\cos \,t \,dt=-1\),
      

      \(\displaystyle \int_{-\pi}^{\,\pi}\,f(t)\,\sin\,t\, dt=3\), \(\displaystyle \int_{-\pi}^{\,\pi}\,f(t)\,\sin\,2t\, dt=4\).

2. 1. Show that the following functions are periodic with period 6: \(\displaystyle \cos\,\frac{\pi}{3} t\), \(\displaystyle \sin\,\frac{\pi}{3} t\), \(\displaystyle \cos\,\frac{2 \pi}{3} t\).
      
      
   2. Show that for any positive integer \(n\) the functions \(\sin\,\frac{n \pi}{3} t\) and \(\cos\,\frac{n \pi}{3} t\) are periodic with period 6.
3. Look again at the trigonometric identity \(\cos^2\,t= \frac{1}{2} (1+\cos\,2t)\). This is itself an example of representation of a periodic function, \(\cos^2 t\), as a combination of elementary periodic functions, \(1\) and \(\cos\,2t\). Use Figure P1 to explain the significance of the \(2\) in \(\cos\,2t\), of the addition of a constant to \(\cos\,2t\), and of the coefficient \(1/2\).
   

   
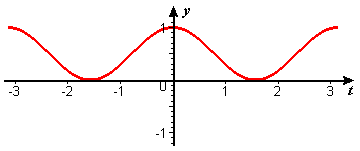
   Figure P1   Graph of \(y=\cos^2\, t\)

4. 1. There are infinitely many functions \(y=f(x)\) defined implicitly by the equation

      \(\displaystyle \sin^2\left(\frac{x}{2}\right)+\cos^2\left(\frac{y}{2}\right)=1\).

      Solve this equation for \(y\) to find one such function. Use the Graph tool to graph the solution you selected.
   2. If you haven't already done so, show that there is a function \(y=f(x)\) defined by this equation that has domain \((-\infty,\infty)\) and that has the properties shown in Figure P2: It is even and periodic with period \(2\pi\).
      

      
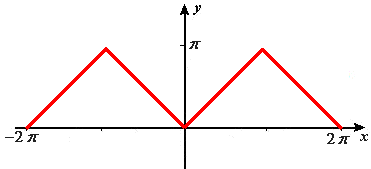
      Figure P2   Triangular wave function

   Unlikely as it may seem, we are going to represent the triangle wave function \(f(x)\) approximately by a trigonometric polynomial of the form \(b_0+b_1 \cos x+b_2 \cos 2x\). That is, we want to find coefficients \(b_0\), \(b_1\), and \(b_2\) so that \(b_0+b_1 \cos x+b_2 \cos 2x\) will approximate \(f(x)\).

   3. Find \(b_0\) by integrating both sides of \(f(x)=b_0+b_1 \cos x+b_2 \cos 2x\) from \(-\pi\) to \(\pi\). You should be able to write down the integral of \(f(x)\) by inspection from Figure P2. In fact, you may be able to guess \(b_0\) from the picture.
      
      
   4. To find additional coefficients, we need to know how to evaluate integrals such as \(\displaystyle\int_{-\pi}^{\pi} f(x)\,\cos x\,dx\). Because both \(f(x)\) and \(\cos\,x\) have even symmetry, this integral is the same as \(\displaystyle 2 \int_0^{\pi} f(x)\,\cos x\,dx\). And, on the interval \([0,\pi]\), \(f(x)\) is just \(x\) (see Figure P2). Thus

      \(\displaystyle\int_{-\pi}^{\pi} f(x)\,\cos x \,dx = 2 \int_0^{\pi} x\,\cos x\,dx\).

      Use integration by parts to evaluate the integral on the right.
      
      
   5. Solve for \(b_1\) and \(b_2\) as you did in Activity 4.
      
      
   6. Reality check: Graph the function \(f(x)=b_0+b_1 \cos x+b_2 \cos 2x\) with your calculated values for \(b_0\), \(b_1\), and \(b_2\), and compare this graph with Figure P2. You should see the approximating graph snake along the triangular wave function.