Acknowledgments

During the winter of 1968-69, the United States was swept by a virulent new strain of influenza, named Hong Kong flu for its place of discovery. At that time, no flu vaccine was available, so many people were infected. We will study the spread of the disease through a single urban population, that of New York City.

In particular, in this project we will examine a mathematical model for the spread of a disease like influenza that is communicated primarily by person-to-person contact. We will see how well this model matches the data we have for the Hong Kong flu in New York City in 1968-69. Then we will look at what the model tells us about vaccination campaigns against diseases such as influenza, rubella (German measles), polio, and smallpox, that are spread by person-to-person contact and such that individuals who recover from the disease have immunity for life.

The name "SIR Model" refers to a division of the population into three mutually exclusive groups: the susceptible population \(S\), the infected population \(I\), and the recovered population \(R\). For the Hong Kong flu in New York City in 1968, we know that the total population was approximately \(7,900,000\). The crucial variable is \(I\), the number of infecteds at different times, which was difficult to determine because a large number of ill people did not go to a doctor and so were unreported. The available data (Figure 1 and Table 1) consist of weekly totals of excess pneumonia-influenza deaths, that is, the number of such deaths in excess of the average number to be expected from other causes. Those who die as a result of the disease probably will not do so right away. We assume that the number of excess deaths is proportional to the number of infected individuals from a couple of weeks before.

Week Flu-related deaths Week Flu-related deaths 1 14 8 108 2 28 9 68 3 50 10 77 4 66 11 33 5 156 12 65 6 190 13 24 7 156
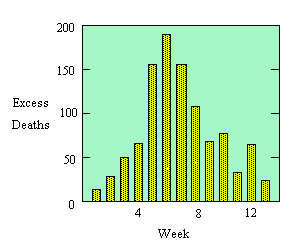Table 1	Figure 1