The argument leading to a length formula for a parabolic curve is not limited to the case of \(f(x)=x^2\) or to the interval \([0,2]\). The same "subdivide and conquer" argument establishes the general formula for the length of the graph of \(y=f(x)\) (where \(f\) is any function with a continuous first derivative) over the interval \(a \leq x \leq b\):

Length of curve ⁢ = ∫ a b 1 + [ f ′ ( x ) ] 2 d ⁢ x .

If this formula is correct, then it should calculate the same length for a circle of radius \(r\) (also known as circumference) as the one you know already, \(2 \pi r\). But we have to take into consideration that a circle is not the graph of a function, so we need to apply the formula to a portion of the circle that is the graph of a function. As we see in Figure P3, the upper semicircle won't work either, because the derivative does not exist at the end points.

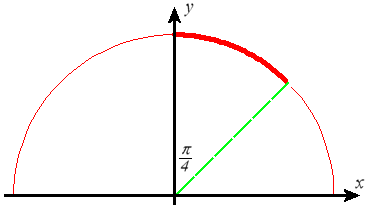
Figure P3  The upper half of a circle

The semicircle in Figure P3 has equation \(x^2+y^2=r^2, \;\; y \geq 0\), or \(y=\sqrt{r^2-x^2}\). We can select one-quarter of the semicircle (one-eighth of the entire circle), as highlighted in red, by taking \(x\) from \(0\) to the intersection with the line \(y=x\).

1. Verify that the point of intersection with \(y=x\) is \(\left(\frac{r}{\sqrt{2}},\frac{r}{\sqrt{2}}\right)\). Thus the integral that gives \(1/8\) of the total length (circumference) of the circle is

⁢ ∫ 0 r / 2 1 + ( d ⁢ y d ⁢ x ) 2 d ⁢ x .

2. Show that the circumference of the circle is

⁢ 8 ⁢ r ⁢ ∫ 0 r / 2 d ⁢ x r 2 - x 2 .

The integral in step 2 can be evaluated using the Fundamental Theorem (i.e., by finding an indefinite integral first) exactly as we did in Example 2 in Section 8.4. The technique is called trigonometric substitution.

3. Evaluate the integral in step 2, and show that the result agrees with what you already know the circumference of the circle to be.