Prerequisite for this page: The first two pages of Project 1 in Chapter 5.

The formula

Length of curve ⁢ = ∫ a b 1 + [ f ′ ( x ) ] 2 d ⁢ x

often leads to integrals that cannot be evaluated by using the Fundamental Theorem, that is, by finding an explicit formula for an indefinite integral. There is such a formula for the case of a parabolic arc, but it's not easy to find. For the circular arc, you found the formula by using a trigonometric substitution. In this part of the project, we will find that the properties of hyperbolic trig functions lead to a very simple integral for the length of a hanging chain or cable (also known as a catenary).

We saw the image at the right in Project 1 in Chapter 5, as an illustration of the catenary shape frequently seen in high-power transmission lines. Because of the lighting, we see the curved lines very clearly. But the shape is distorted somewhat by the angle of our view, almost along the lines. In the image below, the transmission lines don't stand out so well, but the shape we see is closer to a real catenary.

Transmission lines at Bonneville Dam, Oregon

Figure P4  Three catenaries

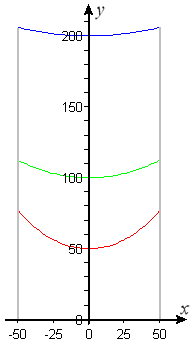With appropriate placement of axes, a catenary is the graph of \(y=a\,\cosh\left(\frac{x}{a}\right)\). Figure P4 shows three such curves with \(a=50\) (red), \(100\) (green), and \(200\) (blue) on the interval \([-50,50]\).

1. Calculate the length of the catenary \(y=a\,\cosh\left(\frac{x}{a}\right)\) on the interval \([-50,50]\). (Your answer will be in terms of \(a\).)
   
   
2. Find the actual length of each of the cables in Figure P4.
   
   
3. Suppose the three curves in Figure P4 represent cables strung (at different heights) between poles that are 100 meters apart. Find the maximum amount of sag in each of the three cables, and compare that maximum sag with the length of the cable in each case. Do the results strike you as paradoxical?

Image credits