Figure P1  Graph of \(y=x^2\)

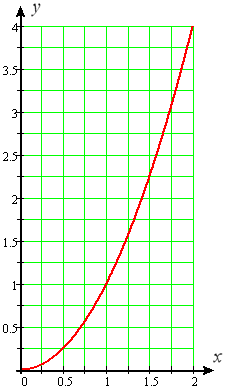In this project we will examine the use of integration to calculate the length of a curve. To have a particular curve in mind, consider the parabolic arc whose equation is \(y=x^2\) for \(x\) ranging from \(0\) to \(2\), as shown in Figure P1.

1. Estimate the length of the curve in Figure P1, assuming that lengths are measured in inches, and each block in the grid is \(1/4\) inch on each side. You may estimate by "eyeballing," or you may use a ruler on your screen. Record your estimate to serve as a check on your later calculation.

Now we think of Figure P1 as the graph of a function, \(f(x)=x^2\) for \(0 \leq x \leq 2\). Suppose we subdivide the interval \([0,2]\) into \(n\) equal parts, each of width \(\Delta x = 2/n\). (Figure P1 displays the case of \(n=8\).) As usual, we denote the partition points by \(x_0, x_1, ..., x_{n-1}, x_n\). Assume that \(n\) is large enough that the portion of the curve in any one subinterval is essentially a straight line. (See Figure P2.)

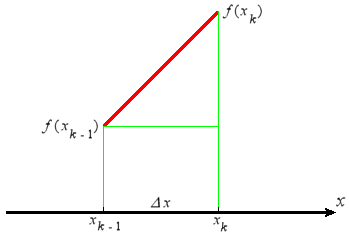
Figure P2  Line segment approximating a curve between two points

2. Explain why the length of the portion of the curve between \(x_{k-1}\) and \(x_k\) can be approximated by

( Δ ⁢ x ) 2 + [ f ′ ( x k - 1 ) Δ ⁢ x ] 2 .

3. Show that the approximation in step 2 leads to this integral formula for the length of the curve:

4. Evaluate the integral in step 3 numerically, using any of the following: an integral key on your calculator, a numerical method from Section 8.3, or an online calculation service. Compare your result with your estimate in step 1 to make sure the numerical result is reasonable. (If you haven't made any mistake in calculating the integral, its value should be much closer to the true length than your estimate.)