In this project we explore the solutions of the differential equation \(y''=\omega^2y\) (where \(\omega\) is a given constant) and related functions. We began this exploration in Section 5.4 with a series of problems that we recommend you work through before working on the project. We summarize here the results of those problems, and on the next page we suggest some reasons why these functions are important.

You can easily check that all functions of the form \(Ae^{\omega t}+Be^{-\omega t}\) are solutions of the differential equation \(y''=\omega^2y\). Furthermore, these are the only solutions, because every initial value problem [with specified values of \(y(0)\) and \(y'(0)\)] must have a solution, and there are only two undetermined constants in the expression \(Ae^{\omega t}+Be^{-\omega t}\).

In Problem 12 in Section 5.4, we defined the hyperbolic sine (abbreviated sinh) and hyperbolic cosine (abbreviated cosh) as two special members of this family of solutions:

\(\sinh\,\omega t=\frac{1}{2}\left(e^{\omega t}-e^{-\omega t}\right)\) and \(\cosh\,\omega t=\frac{1}{2}\left(e^{\omega t}+e^{-\omega t}\right)\).

Figure P1 Graphs of sinh (red),
cosh (blue), and exponential
functions (green)

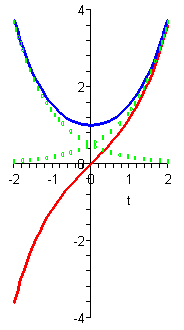In Figure P1 we show these functions (with \(\omega=1\)) and the exponential functions from which they are constructed. The cosh function (in blue) is the sum of the two exponential functions (in green), and the sinh function (in red) is the difference of the exponential functions.

The following equalities are easy to see directly from the definitions of \(\sinh\) and \(\cosh\).

\(\cosh\,\omega t + \sinh\,\omega t = e^{\omega t}\)

\(\cosh\,\omega t - \sinh\,\omega t = e^{-\omega t}\)

If we multiply the left-hand and right-hand sides of these two equations, we find

\(\cosh^2 \omega t - \sinh^2 \omega t = 1\).

Thus, if \(x=\cosh\,\omega t\) and \(y=\sinh\,\omega t\), then \(x^2-y^2=1\). This is an equation of a hyperbola in the \(x,y\)-plane, which is why these functions are called “hyperbolic.”

Also directly from the definitions we see

\(\frac{d}{dt}\,\sinh\,\omega t= \omega\,\cosh\,\omega t\)  and  \(\frac{d}{dt}\,\cosh\,\omega t = \omega\,\sinh\,\omega t\).

If we differentiate again, we see (as we knew already) that \(y=\sinh\,\omega t\) and \(y=\cosh\,\omega t\) are both solutions of \(y''=\omega^2\,y\).