We saw in the Introduction that hyperbolic sine and cosine are functions that are related by formulas similar to the ones for "circular" sine and cosine:

\(\cosh^2\, t - \sinh^2\, t = 1\,\);

\(\frac{d}{dt}\,\sinh\, t = \cosh\,t\)  

\(\frac{d}{dt}\,\cosh\, t = \sinh\, t\)   

Surely there must be a "hyperbolic tangent function" and other "hyperbolic trig" functions close at hand.

1. Write down definitions for the hyperbolic tangent function (\(\tanh\)) and the hyperbolic secant function (\(\text{sech}\)) in terms of \(\sinh\) and \(\cosh\).
2. Express \(\tanh\,t\) and \(\text{sech},t\) in terms of exponential functions.
3. Find an identity relating the squares of \(\tanh\,t\) and \(\text{sech}\,t\).

Figure P4 shows a graph of the hyperbolic tangent function.

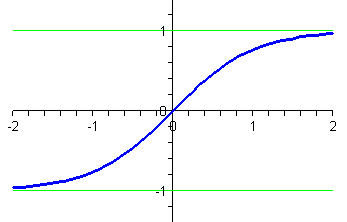
Figure P4  The hyperbolic tangent function

4. Explain the features you see in the graph: all values between \(-1\) and \(1\), increasing on the entire domain, approaching \(y=1\) and \(y=-1\) as asymptotes. Hints: You may want to rewrite the definition of \(\tanh\,t\) in terms of exponential functions. You may also find Figure P1 helpful.
5. Make your own graph of \(y=\text{sech}\,t\). Explain the features you see, including range, asymptotes (if any), max/min values (if any), and intervals where the function is increasing or decreasing. Hint: You should be able to do this without knowing a formula for the derivative of the function.
6. Find the derivative of \(\tanh\,t\), and express the answer in terms of \(\text{sech}\,t\). Hint: You may want to make use of the Quotient Rule.
7. The graph of \(y=\tanh\,t\) in Figure P4 appears to have its steepest slope at the origin. What is that slope? Why?
8. Find the derivative of \(\text{sech}\,t\), and express the answer in terms of \(\tanh\,t\) and \(\text{sech}\,t\). Use your formula to confirm what you found in step 5 regarding intervals of increasing and decreasing behavior, as well as extreme values.
9. Compare the identities and formulas for hyperbolic functions (\(\sinh\), \(\cosh\), \(\tanh\), and \(\text{sech}\)) with the corresponding identities and formulas for trigonometric functions, specifically, the identities relating sine and cosine, tangent and secant, and the derivative formulas for all four functions.
10. (Optional) Define \(\coth\,t\) and \(\text{csch}\,t\). Find an identity relating these two functions. Calculate their derivatives, and graph both functions.