In Figures P5 and P6, we show the graphs of the hyperbolic sine (\(\sinh\)) and the hyperbolic tangent (\(\tanh\)), repeated from Figures P1 and P4, respectively.

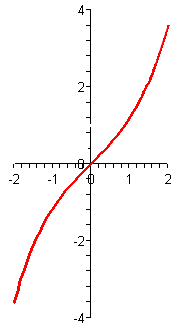Figure P5   Hyperbolic sine

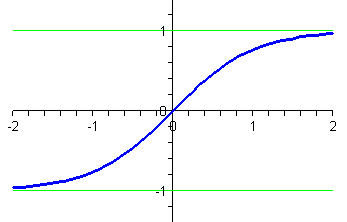Figure P6  Hyperbolic tangent

Each of these functions is clearly invertible, and the graphs of the inverse functions can be found by rotating around the line \(y=x\), as shown in Figures P7 and P8.

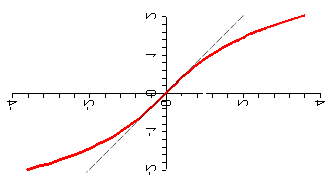Figure P7  Inverse hyperbolic sine

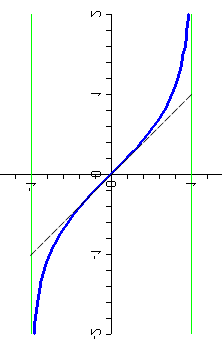Figure P8  Inverse hyperbolic tangent

In one sense, the formulas for the curves shown in Figures P7 and P8 are, respectively, \(y=\sinh^{-1}\,x\) and \(y=\tanh^{-1}\,x\). But that's not particularly helpful, for example, in finding derivatives of these functions. We can do better, because we know formulas for \(\sinh\) and \(\tanh\) in terms of exponentials.

1. What is the domain of \(\sinh^{-1}\,\)? What is the domain of \(\tanh^{-1}\,\)?
2. In Figure P7, \(x=\sinh\,y=\frac{e^y-e^{-y}}{2}\). Solve for \(y\) as a function of \(x\) to find a formula for \(\sinh^{-1}\,x\). [Hints: Before or after clearing the fraction, multiply both sides by \(e^y\). This will produce a quadratic equation in which the variable is \(e^y\). The Quadratic Formula appears to produce two solutions, but only one of them makes sense.]
3. In Figure P8, \(x=\tanh\,y=\frac{e^y-e^{-y}}{e^y+e^{-y}}\). Solve for \(y\) as a function of \(x\) to find a formula for \(\tanh^{-1}\,x\). [Hint: First multiply numerator and denominator by \(e^y\).]
4. Find a formula for the derivative of \(y=\sinh^{-1}\,x\). [Hints: You could do this directly from the formula you found in 2, but it's easier to do it implicitly from \(\sinh\,y=x\). To express the answer in terms of \(x\), use the formula \(\cosh^2\,x - \sinh^2\,x=1\), but be careful with the sign when you take a square root.]
5. Find a formula for the derivative of \(y=\tanh^{-1}\,x\). [Hint: Use a property of the natural logarithm to simplify the calculation.]

In the second part of this project, we saw the importance of the hyperbolic cosine as a modeling tool, but we are not emphasizing it here, because it is not an invertible function on its entire domain. (See Figure P1 again.) We could restrict its domain to non-negative numbers and do similar calculations of formulas for the inverse function and its derivative, but it's not particularly useful to do so. Note that, in our kite string example, the inverse function required for calculation is \(\sinh^{-1}\).